✍ 스프레드시트를 이용한 통계 - 대푯값·산포도
스프레드시트를 이용하여 대푯값과 산포도를 구해보자.
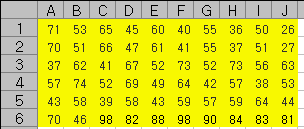
❖ 그림과 같이 초기 자료를 입력한다.
❖ 평균: "=AVERAGE(자료가 입력된 범위)"
주어진 예에서는 "=AVERAGE(A1:J6)"
❖ 도수분포표에서의 평균: 실질적으로 자료가 주어진 경우에는 바로 평균을 구할 수 있기 때문에 도수분포표에서의 평균은 그 의미가 약하다. 도수분표표에서의 평균은 ((계급값)*(도수)의 총합)/(계급의 수)이므로 다음과 같이 구할 수 있다.
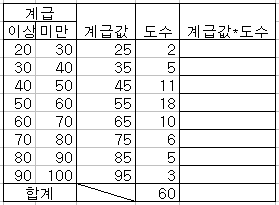
• 예를 들어 첫 번째 계급의 계급값이 F10 셀에 있다면 "계급값*도수"란에는 "=F10*G10"이라 입력한다.
• 나머지 셀을 채우기 위해 자동 채우기 기능을 사용한다.
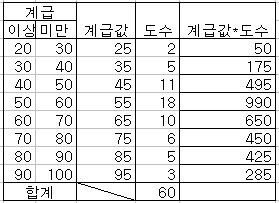
• "계급값*도수"의 총합을 "=SUM(범위)"을 이용하여 계산한다.
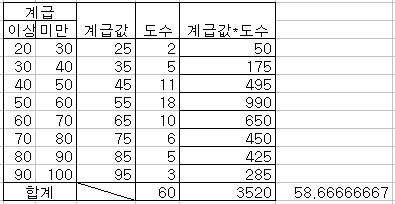
• 평균값을 입력할 셀에 "=계급값*도수의 총합이 계산된 셀/도수의 총합이 계산된 셀"을 입력한다.
주어진 예에서는 도수의 총합이 입력된 셀이 G18이므로 "=H18/G18"이 된다.
❖ 분산: "=VAR.P(자료가 입력된 범위)"
주어진 예에서는 "=VAR.P(A1:J6)"
❖ 표준편차: "=STDEV.P(자료가 입력된 범위)"
주어진 예에서는 "=STDEV.P(A1:J6)"
❖ 최빈값-가장 많이 발생한 수: "=MODE.SNGL(자료가 입력된 범위)"
주어진 예에서는 "=MODE.SNGL(A1:J6)"
❖ 중앙값: "MEDIAN(자료가 입력된 범위)"
주어진 예에서는 "=MEDIAN(A1:J6)"
❖ 사분위수: 변량 X의 n개의 관측값을 작은 쪽으로부터 크기 순으로 배열했을 때전체 관측값을 4등분하는 위치에 오는 값을 말한다. 제2사분위수는 중앙값과 제4사분위수는 최댓값과 같다. "=QUARTILE.INC(자료가 입력된 범위,0~4)"
주어진 예에서 제2사분위수는 "=QUARTILE.INC(A1:J6,2)"
 <
<