❦ 삼각비

❧ 삼각비의 뜻

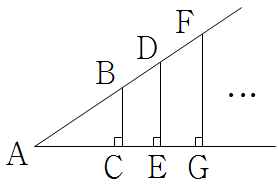
$\rm {\triangle ABC \backsim \triangle ADE \backsim \triangle AFG = \cdots }$

▶ $\sin A=\rm {\dfrac {\overline {BC }}{\overline {AB } }=\dfrac {\overline {DE }}{\overline {AD } }=\dfrac {\overline {FG }}{\overline {AF } } }=\cdots$ ▶ $\cos A=\rm {\dfrac {\overline {AC }}{\overline {AB } }=\dfrac {\overline {AE }}{\overline {AD } }=\dfrac {\overline {AG }}{\overline {AF } } }=\cdots$ ▶ $\tan A=\rm {\dfrac {\overline {BC }}{\overline {AC } }=\dfrac {\overline {DE }}{\overline {AE } }=\dfrac {\overline {FG }}{\overline {AG } } }=\cdots$

 

❧ $30^\circ ,~45^\circ ,~60^\circ$의 삼각비의 값

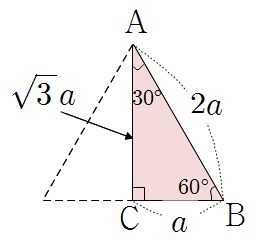
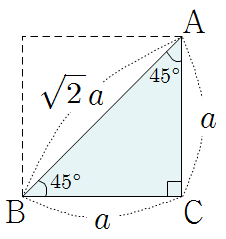
	$30^\circ$	$45^\circ$	$60^\circ$
$\sin A$	$\dfrac12$	$\dfrac { \sqrt2}2$	$\dfrac { \sqrt3}2$
$\cos A$	$\dfrac { \sqrt3}2$	$\dfrac { \sqrt2}2$	$\dfrac12$
$\tan A$	$\dfrac1 {\sqrt3 }$	$1$	$\sqrt3$

 

❧ 예각의 삼각비의 값

 

	$0^\circ$	$90^\circ$
$\sin A$	$0$	$1$
$\cos A$	$1$	$0$
$\tan A$	$0$	정할 수 없다.

 

❧ 삼각비의 표

각도	$\sin$	$\cos$	$\tan$
$0^\circ$	$0.0000$	$1.0000$	$0.0000$
$1^\circ$	$0.0175$	$0.9998$	$0.0175$
$2^\circ$	$0.0349$	$0.9994$	$0.0349$
$3^\circ$	$0.0523$	$0.9986$	$0.0524$
$\cdots$	$\cdots$	$\cdots$	$\cdots$
$29^\circ$	$0.4848$	$0.8746$	$0.5543$
$30^\circ$	$0.5000$	$0.8660$	$0.5774$
$31^\circ$	$0.5150$	$0.8572$	$0.6009$
$\cdots$	$\cdots$	$\cdots$	$\cdots$
$45^\circ$	$0.7071$	$0.7071$	$1.0000$
$\cdots$	$\cdots$	$\cdots$	$\cdots$
$60^\circ$	$0.8660$	$0.5000$	$1.7321$
$\cdots$	$\cdots$	$\cdots$	$\cdots$
$88^\circ$	$0.9994$	$0.0349$	$28.6363$
$89^\circ$	$0.9998$	$0.0175$	$57.2900$
$90^\circ$	$1.0000$	$0.0000$

각도 : $A=$$^\circ$   

 

❦ 삼각비의 활용

❧ 삼각비와 변의 길이의 관계

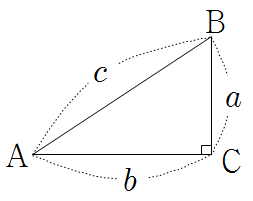
• $\sin A=\dfrac ac\quad\implies\quad a=c\sin A$
• $\cos A=\dfrac bc\quad\implies\quad b=c\cos A$
• $\tan A=\dfrac ab\quad\implies\quad a=b\tan A$

 

❧ 삼각형의 넓이

▶ $\angle \rm A$가 예각일 때,

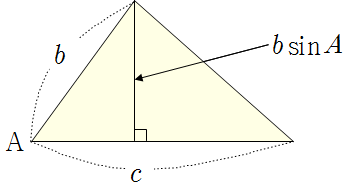
$S=\dfrac12 bc\sin A$

 

▶ $\angle \rm A$가 둔각일 때,

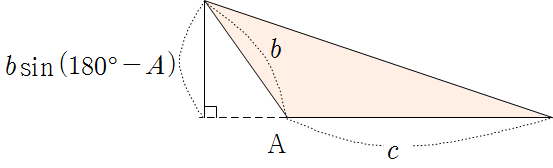
$S=\dfrac12 bc\sin (180^\circ -A)$