❦ 피타고라스 정리의 활용(평면)

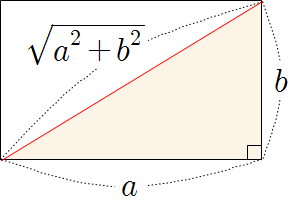
❧ 직사각형의 대각선의 길이

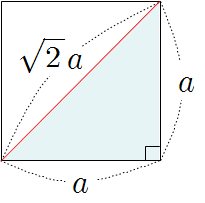
<직사각형>	<정사각형>

 

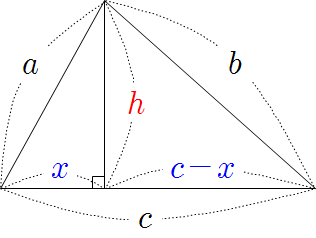
❧ 삼각형의 높이

\(\begin {cases} h^2=a^2 -x^2 \\h^2 =b^2 - (c-x)^2\end {cases}\)

 

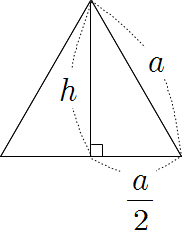
❧ 정삼각형의 높이와 넓이

\(\eqalign {h&=\sqrt {a^2 - \left(\frac a2 \right)^2 }\\&=\frac {\sqrt3}2 a \\\\S&=\frac12 ah\\&=\frac {\sqrt3}4 a^2 }\)

 

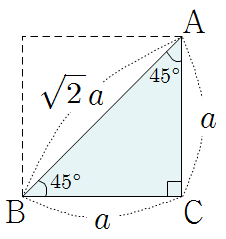
❧ 직각삼각형의 세 변의 길이의 비

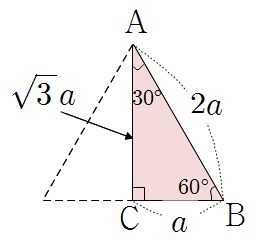
\(\begin {align*}&\rm {\overline {AB }\, :\,  \overline {BC }\,  :\,  \overline {CA } }\\ &=\sqrt 2a\, :\, a\, :\, a\\&=\sqrt 2\, :\, 1\, :\, 1\end {align*}\)	\(\begin {align*}&\rm {\overline {AB }\, :\,  \overline {BC }\,  :\,  \overline {CA } }\\ &=2a\, :\, a\, :\,\sqrt 3 a\\&=2\, :\, 1\, :\, \sqrt 3\end {align*}\)

 

❧ 좌표평면 위의 두 점 사이의 거리

 

❦ 피타고라스 정리의 활용(입체)

❧ 직육면체의 대각선의 길이

\(l=\sqrt {a^2+b^2+c^2 }\)

 

❧ 원뿔의 높이

\(h=\sqrt {l^2-r^2 }\)

 

❧ 구의 반지름

 

❧ 사각뿔의 높이

 

❧ 정사면체의 높이와 부피