❦ 피타고라스 정리

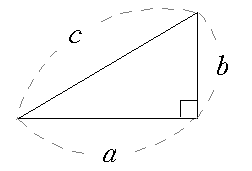
❧ 피타고라스 정리 : 직각삼각형의 직각을 낀 두 변의 길이를 각각 \(a,~b\)라 하고, 빗변의 길이를 \(c\)라고 하면\[a^2+b^2=c^2\]이다.

♠ How to... 점 \(\mathrm { B,~C}\)를 끌어보면서 정사각형의 넓이의 변화를 관찰한다.

 

❧ 피타고라스 정리의 증명

▶ 합동인 네 개의 직각삼각형을 이용

♠ How to... 합동인 삼각형과 사각형의 넓이를 이용하여 정리가 성립함을 확인한다.

 

▶ 삼각형 블럭을 이동

♠ How to... 점 \(\mathrm { A,~B,~C}\)를 끌어 모양을 정리하여 확인한다. 슬라이드 \(e\)를 끌어 삼각형의 크기를 조절한다.

 

▶ 바스카라(Bhaskara, 1114~1185)의 증명

♠ How to... 점 \(\mathrm { A,~B}\)를 끌어 모양을 정리하여 확인한다. 슬라이드 \(a,~b\)를 끌어 삼각형의 크기를 조절한다.

 

▶ 유클리드(Euclid, B.C.325?~B.C.265?)의 증명

♠ How to... 슬라이드 \(\mathrm { X,~Y}\)를 순서대로 끌어 증명을 이해한다.

 

♠ How to... 슬라이드 \(\mathrm { X,~Y}\)를 순서대로 끌어 증명을 이해한다.

 

▶ 레오나르도 다빈치의 증명

♠ How to... check1,2,3를 이용하여 증명을 이해한다.

 

▶ 구고현(勾股弦)의 정리

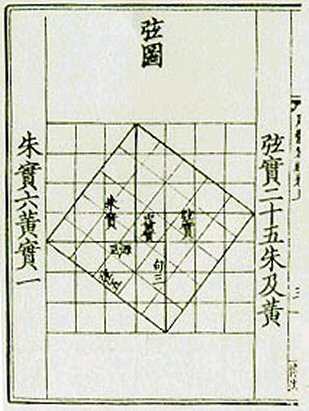\((구)^2+(고)^2=(현)^2\)

 

▶ 아나리지(Annairizi of Arabia, ca. 900 A.D.)의 증명

 

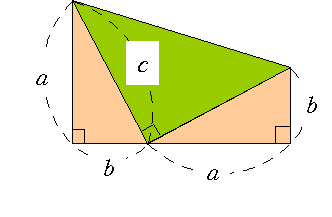
▶ 가필드(James Abram Garfield, 1831 ~ 1881)의 증명

▶ 닮음을 이용한 증명

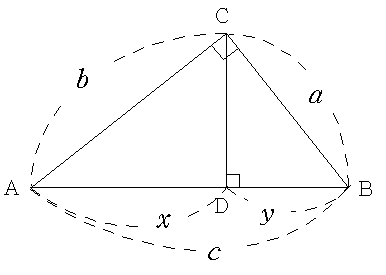
\(\mathrm { \triangle ACD \backsim \triangle ABC,~\triangle BCD \backsim \triangle BAC}\)

 

❦ 직각삼각형이 될 조건

❧ 삼각형의 세 변의 길이가 각각 \(a,~b,~c\)인 \(\triangle \mathrm { ABC}\)에서\[a^2+b^2=c^2\]이면 이 삼각형은 빗변의 길이가 \(c\)인 직각삼각형이다.

 

❧ 피타고라스의 세 쌍

자연수의 순서쌍만 출력합니다.

결과확인 \(a=\)   \(b=\)   \(c=\)   \(a^2+b^2=\) \(c^2=\)

▶ 세 쌍을 구하는데 사용한 식

\(a=2pq,~b=p^2-q^2,~c=p^2+q^2\)
(단, \(p> q,~p,~q\)는 자연수)