인수분해

✾ 인수분해

❦ 인수분해의 뜻

❧ 인수분해

▶ 하나의 다항식을 두 개 이상의 다항식의 곱으로 나타낼 때, 각각의 식을 처음 식의 인수라고 한다. 또, 하나의 다항식을 두 개 이상의 인수의 곱으로 나타내는 것을 그 다항식을 인수분해한다고 한다.

☞ \(x+1,~x+2\)는 \(x^2+3x+2\)의 인수

❧ 인수분해하는 일반적인 방법

다항식 \(ma+mb\)에서 \(m\)은 항 \(ma,~mb\)에 공통으로 들어있는 인수이다. 이와 같이 공통인 인수가 있을 때에는 분배법칙을 이용하여 다음과 같이 인수분해한다.\[ma+mb=m(a+b)\]

❦ 인수분해 공식

❧ 곱셈공식에서 좌변과 우변을 서로 바꾸어 놓으면 인수분해 공식을 얻는다.

❧ \(\begin {align}a^2+2ab+b^2=(a+b)^2\\a^2-2ab+b^2=(a-b)^2\end {align}\)

❧ 완전제곱식 : \((x+y)^2,~2(x-1)^2,~-(x+2y)^2\)과 같이 다항식의 제곱으로 이루어진 식 또는 이 식에 상수를 곱한 식을 완전제곱식이라고 한다.

※ \(x^2+ax+b=(x+k)^2\)꼴로 인수분해되기 위한 조건

⇒ \(b=\left(\dfrac12 a\right)^2\)

❧ \(a^2-b^2=(a+b)(a-b)\)

❧ \(x^2+(a+b)x+ab=(x+a)(x+b)\)

❧ \(acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\)

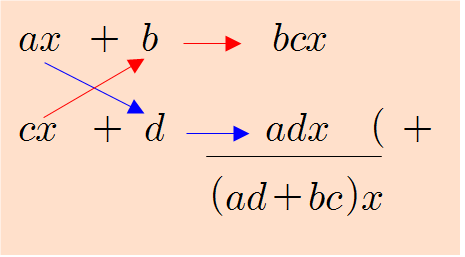
☞ 한 걸음 더

Home