❦ 제곱근의 곱셈과 나눗셈

❧ 제곱근의 곱셈

\(a>0,\enspace b>0\)일 때,

▶ \(\sqrt a \sqrt b =\sqrt { ab}\)

▶ \(\sqrt { a^2 b}=a\sqrt b\)

 

❧ 제곱근의 나눗셈

\(a>0,\enspace b>0\)일 때,

▶ \(\dfrac { \sqrt a} { \sqrt b}=\sqrt { \dfrac ab}\)

 

❧ 분모의 유리화 : 분수의 분모에 근호가 있을 때, 분자와 분모에 \(0\)이 아닌 같은 수를 곱하여 분모를 유리수로 고치는 것

일반적으로 \(a>0,\enspace b>0\)일 때,

▶ \(\dfrac { \sqrt a} { \sqrt b}=\dfrac { \sqrt a \times \sqrt b} { \sqrt b \times \sqrt b}=\dfrac { \sqrt { ab}} { b}\)

예) \(\dfrac { \sqrt 3} { \sqrt 2}=\dfrac { \sqrt 3 \times \sqrt 2} { \sqrt 2 \times \sqrt 2}=\dfrac { \sqrt { 6}} { 2}\)

     \(\dfrac { 1} { \sqrt { 12}}=\dfrac { 1} { 2\sqrt3}=\dfrac { 1\times \sqrt3} { 2\sqrt3 \times \sqrt3}=\dfrac { \sqrt3} { 6}\)

 

❦ 제곱근의 덧셈과 뺄셈

❧ 제곱근의 덧셈과 뺄셈 : 제곱근의 덧셈과 뺄셈은 다항식의 덧셈과 뺄셈에서 동류항끼리 모아서 계산한 것과 같은 방법으로 근호 안의 수가 같은 것끼리 모아서 계산한다.

 

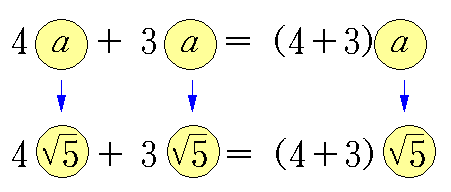
❧ 근호를 포함한 사칙계산 : 근호를 포함한 식에 덧셈, 뺄셈, 곱셈, 나눗셈이 섞여 있을 때에는 유리수와 마찬가지로 곱셈과 나눗셈을 먼저 계산한 후 덧셈과 뺄셈을 계산한다.

\(\begin {align}예) \sqrt2 \times \dfrac { \sqrt3} { 2}-\sqrt3 \times \sqrt2 &=\dfrac { \sqrt6}{ 2}-\sqrt6\\&=\dfrac { \sqrt6} { 2}-\dfrac { 2\sqrt6} { 2}\\&=-\dfrac { \sqrt6} { 2}\end {align}\)

 

❧ 곱셈 공식을 이용한 분모의 유리화

\((a+b)(a-b)=a^2-b^2\)을 이용하여 분모에 근호가 있는 분수의 분모를 유리화할 수 있다.

예) \(\dfrac { 1} { \sqrt2 +1}=\dfrac { 1\times(\sqrt2-1)} { (\sqrt2+1)(\sqrt2-1)}=\dfrac { \sqrt2-1} { 2-1}=\sqrt2-1\)

 

❦ 실수의 대소 관계

❧ 두 실수 \(a,~b\)에 대하여

▶ \(a-b>0\)이면 \(a>b\)

▶ \(a-b=0\)이면 \(a=b\)

▶ \(a-b<0\)이면 \(a<b\)

  예) \(\sqrt2+1\)과 \(3-\sqrt2\)의 대소 비교

      \(\begin {align}(\sqrt2+1)-(3-\sqrt2)&=\sqrt2+1-3+\sqrt2\\&=2\sqrt2-2\\&=\sqrt8-\sqrt4>0\end {align}\)

      따라서 \(\sqrt2+1 > 3-\sqrt2\)

 

❦ 제곱근의 값

❧ 제곱근표를 이용한 제곱근의 값

▶ 제곱근표를 이용하여 반올림하여 소수점 아래 셋째 자리까지의 값을 구할 수 있다.

▶ 제곱근의 성질을 이용하여 제곱근표에 나오지 않은 수는 다음과 같이 구할 수 있다.

예) \(\sqrt { 200}=\sqrt { 10^2 \times2}=10\sqrt2 \fallingdotseq 10\times1.414=14.14\)

      \(\sqrt { 3000}=\sqrt { 10^2 \times30}=10\sqrt 30 \fallingdotseq 10\times5.477=54.77\)

▶ 제곱근표

	0	1	2	3	4	5	6	7	8	9
1.0	1.000	1.005	1.010	1.015	1.020	1.025	1.030	1.034	1.039	1.044
1.1	1.049	1.054	1.058	1.063	1.068	1.072	1.077	1.082	1.086	1.091
1.2	1.095	1.100	1.105	1.109	1.114	1.118	1.122	1.127	1.131	1.136
1.3	1.140	1.145	1.149	1.153	1.158	1.162	1.166	1.170	1.175	1.179
…	…	…	…	…	…	…	…	…	…	…
2.0	1.414	1.418	1.421	1.425	1.428	1.432	1.435	1.439	1.442	1.446
…	…	…	…	…	…	…	…	…	…	…
3.0	1.732	1.735	1.738	1.741	1.744	1.746	1.749	1.752	1.755	1.758
…	…	…	…	…	…	…	…	…	…	…
9.9	3.146	3.148	3.150	3.151	3.153	3.154	3.156	3.158	3.159	3.161
10	3.162	3.178	3.194	3.209	3.225	3.240	3.256	3.271	3.286	3.302
11	3.317	3.332	3.347	3.362	3.376	3.391	3.406	3.421	3.435	3.450
12	3.464	3.479	3.493	3.507	3.521	3.536	3.550	3.564	3.578	3.592
13	3.606	3.619	3.633	3.647	3.661	3.674	3.688	3.701	3.715	3.728
…	…	…	…	…	…	…	…	…	…	…
99	9.950	9.955	9.960	9.965	9.970	9.975	9.980	9.985	9.990	9.995