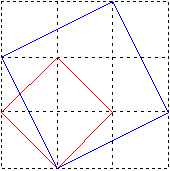
❦ 제곱근의 뜻
❧ 제곱근 : 어떤 수 \(x\)를 제곱하여 \(a\)가 될 때, 즉\[x^2=a\]일 때, \(x\)를 \(a\)의 제곱근이라고 한다.
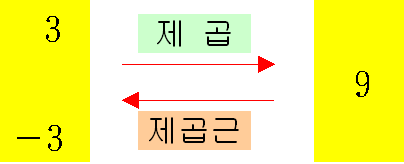
☞ 양수나 음수를 제곱하면 항상 양수이므로 음수의 제곱근은 생각하지 않는다. 또, 제곱하여 \(0\)이 되는 수는 \(0\)뿐이므로 \(0\)의 제곱근은 \(0\)이다.
❧ 제곱근의 표현
▶ 양수 \(a\)의 두 제곱근 중에서 양수인 것을 양의 제곱근, 음수인 것을 음의 제곱근이라 하고, 기호 \(\sqrt {\enspace}\)를 사용하여 \[\sqrt a ,\quad-\sqrt a \]와 같이 나타낸다. 또, \(\sqrt a\)와 \(-\sqrt a\)를 한꺼번에 \(\pm\sqrt a\)로 나타내기도 한다.
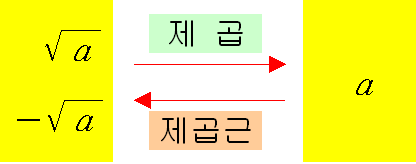
▶ 기호 \(\sqrt {\enspace}\)를 근호라 하고, \(\sqrt a\)를 '제곱근 \(a\)' 또는 '루트 \(a\)'라고 읽는다.
예) \(5\)의 양의 제곱근은 \(\sqrt5\), 음의 제곱근은 \(-\sqrt5\)이므로 \(5\)의 제곱근은 \(\pm\sqrt5\)이다.

† \(\pm\sqrt a\)를 '플러스 마이너스 루트 \(a\)'라고 읽는다.
† '제곱근 \(a\)'와 '\(a\)의 제곱근'의 차이
• 제곱근 \(a\) : \(\sqrt a\)
• \(a\)의 제곱근 : \(\sqrt a ,\enspace-\sqrt a\)
❦ 제곱근의 성질과 대소 관계
❧ 제곱근의 성질
\(a>0\)일 때
▶ \((\sqrt a )^2=a,\quad(-\sqrt a )^2 =a\)
▶ \(\sqrt { a^2} =a,\quad\sqrt { (-a)^2} =a\)
※ \(\sqrt { a^2}=|a|=\begin {cases} a \quad&(a\geq0 일~때)\\-a&(a<0 일~때)\end {cases}\)
❧ 제곱근의 크기 비교
\(a>0,\enspace b>0\)일 때
▶ \(a<b\)이면 \(\sqrt a < \sqrt b\)
▶ \(\sqrt a<\sqrt b\)이면 \(a<b\)
|
|
☜ \(\sqrt2\)와 \(\sqrt5\)의 크기 비교 |

† 제곱근의 대소 비교는 제곱근의 성질을 이용하여 근호 안의 수의 크기를 비교한다.
예) \(2\sqrt3\)과 \(\sqrt { 10}\)의 대소 비교
⇒ \(2\sqrt3 = \sqrt { 2^2}\sqrt3 =\sqrt { 2^2 \times 3}=\sqrt { 12}\)이므로 \(2\sqrt3 >\sqrt { 10}\)
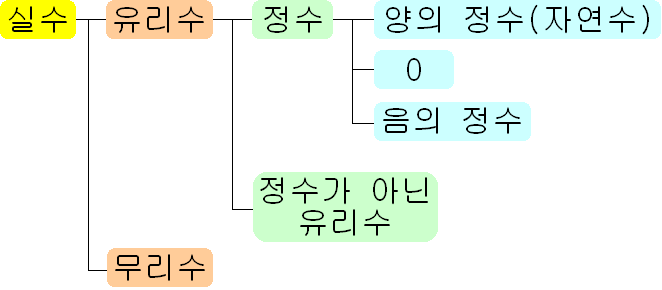
❦ 무리수와 실수
❧ 무리수 : \(\sqrt2\)와 같이 유리수가 아닌 수를 무리수라고 한다. 무리수는 순환하지 않는 무한소수로 나타내어짐이 알려져 있다.
\(1<2<4\)이므로 \(\sqrt1 < \sqrt2 <\sqrt4\), 즉 \(1<\sqrt2 <2\)
따라서 \(\sqrt2\)는 정수가 아니다.
정수가 아닌 유리수는 \(\dfrac { b} { a}\) (\(a,\enspace b\)는 서로소인 정수, \(a\neq0\))의 꼴로 나타낼 수 있는데, 기약분수의 제곱은 기약분수이므로 정수가 아니다.
따라서 \(\sqrt2\)를 기약분수로 나타낼 수 있다면 \((\sqrt2)^2\)은 정수가 아니어야 한다. 하지만 \((\sqrt2)^2\)은 정수이므로 \(\sqrt2\)는 기약분수로 나타낼 수 없다.
그러므로 \(\sqrt2\)는 정수도 아니고, 기약분수로도 나타낼 수 없으므로 유리수가 아니다.

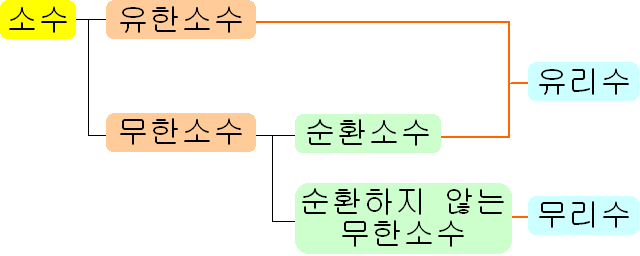
† 유한소수 또는 순환소수로 나타낼 수 있는 수는 유리수이다.
† 무리수의 예) \(\sqrt3 ,\enspace\pi ,\enspace 1+\sqrt2 ,\enspace0.1010010001\cdots \) 등
† 근호 안의 수가 유리수의 제곱이 되지 않는 수이면 무리수이다.
예) \(\sqrt4=\sqrt { 2^2}=2\quad\) 유리수
\(\sqrt { 12}=\sqrt { 2^2 \times3}=2\sqrt3 \quad\) 무리수
❧ 실수 : 유리수와 무리수를 통틀어 실수라고 한다.
❧ 수직선 위에서의 무리수
- 점 \(\mathrm A\)를 끌어보고, 체크박스 p, q를 클릭하면서 관찰한다.
|
♠ How to... |
수직선 위에는 유리수에 대응하는 점들 뿐만 아니라 무리수에 대응하는 점들도 존재한다.
일반적으로 수직선은 유리수와 무리수에 대응하는 점들로 완전히 메울 수 있음이 알려져 있다.
☞ 한 걸음 더
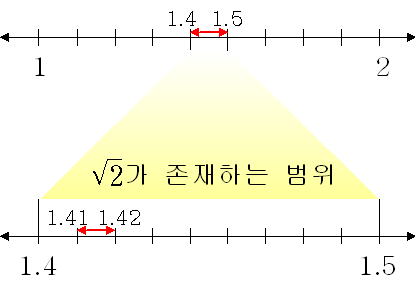
♠ \(\sqrt2\)를 소수로 나타내기
\(1^2<2<2^2\)이므로 \(1<\sqrt2 <2\)
\(1.4^2<2<1.5^2\)이므로 \(1.4<\sqrt2 <1.5\)
\(1.41^2 <2<1.42^2\)이므로 \(1.41<\sqrt2 <1.42\)
이와 같은 방법을 계속 반복하면 \(\sqrt2=1.4142135\cdots\)와 같이 순환하지 않는 무한소수가 됨을 알 수 있다.
♠ 계산기를 이용한 제곱근의 값
|
|
• \(\sqrt2\)의 값을 구하고자 한다면 '\(2\)'를 누르고 '\(\sqrt { \phantom 1}\)' 버튼을 누른다. • 계산기의 종류에 따라 표현할 수 있는 소수점 아래의 자릿수는 달라진다. |
Copyright © 2003-2017 trsketch. All Rights Reserved. trsketch.dothome.co.kr
Saturday, July 18, 2015