닮음의 활용

✾ 닮음의 활용

❦ 평행선 사이의 선분의 길이의 비

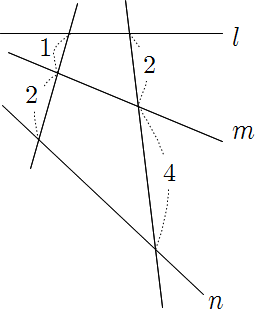
❧ 세 평행선이 다른 두 직선과 만날 때, 평행선 사이의 선분의 길이의 비는 같다. 즉,

\(l\mathrel {/\!/}m\mathrel {/\!/}n\)이면 \(a\,:\,b=c\,:\,d\)

♠ How to...

† '\(a\,:\,b=c\,:\,d\)이면 \(l\mathrel {/\!/}m\mathrel {/\!/}n\)이다.'는 거짓이다.

❦ 삼각형의 무게중심

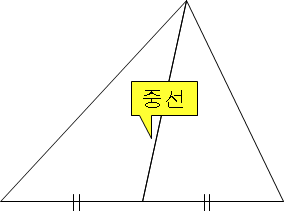
❧ 중선 : 삼각형에서 한 꼭짓점과 그 대변의 중점을 이은 선분

❧ 삼각형의 무게중심

▶ 삼각형의 세 중선은 한 점(무게중심)에서 만난다.

▶ 삼각형의 무게중심은 중선의 길이를 각 꼭짓점으로부터 각각 \(2\,:\,1\)로 나눈다.

▶ 삼각형의 세 중선에 의하여 나누어진 \(6\)개의 삼각형의 넓이는 모두 같다.

\(\rm \triangle ABC\)의 두 중선의 교점을 \(\rm G\)라고 하면

\(\rm \triangle ABC\)와 \(\rm \triangle EDC\)에서

\(\rm\overline {BC}\,:\,\overline {DC}=\overline {AC}\,:\,\overline {EC}=2\,:\,1\)

이고 \(\rm\angle C\)는 공통인 각이므로
\(\rm \triangle ABC\)∽\(\rm \triangle EDC\)이다.

이때 \(\rm \angle BAC=\angle DEC\)이므로
\(\rm \overline {AB}\mathrel {/\!/}\overline {ED}\)이고

\(\rm \overline {AB}\,:\,\overline {ED}=2\,:\,1\)이다.

따라서 \(\rm \triangle GAB\)∽\(\rm \triangle GDE\)이고, 그 닮음비는 \(2\,:\,1\)이므로

\(\rm\overline {AG}\,:\,\overline {GD}=\overline {BG}\,:\,\overline {GE}=2\,:\,1\) … ①
이다.

같은 방법으로 중선 \(\rm CF\)와 중선 \(\rm AD\)와의 교점을 \(\rm G'\)이라고 하면 \(\rm \overline {FD}\mathrel {/\!/}\overline {AC}\)이므로

\(\rm\overline {AG'}\,:\,\overline {G'D}=\overline {CG'}\,:\,\overline {G'F}=2\,:\,1\) … ②
이다.

①, ②에서 두 점 \(\rm G\), \(\rm G'\)은 모두 중선 \(\rm AD\)를 꼭짓점 \(\rm A\)로부터 그 길이가 \(2\,:\,1\)이 되도록 나누는 점이므로 두 점 \(\rm G\)와 \(\rm G'\)은 동일한 점이다.

❦ 닮은 도형의 넓이의 비와 부피의 비

❧ 닮은 평면도형의 넓이의 비는 닮음비의 제곱과 같다.
즉, 닮음비가 \(m\,:\,n\)이면 넓이의 비는 \(m^2\,:\,n^2\)이다.

❧ 닮은 입체도형의 부피의 비는 닮음비의 세제곱과 같다.
즉, 닮음비가 \(m\,:\,n\)이면 부피의 비는 \(m^3\,:\,n^3\)이다.

Home