❦ 도형의 닮음

❧ 도형의 닮음 : 한 도형을 일정한 비율로 확대 또는 축소한 도형이 다른 한 도형과 합동일 때, 그 두 도형은 서로 닮음인 관계에 있다고 하거나 서로 닮은 도형이라고 한다.

▶ \(\rm\triangle ABC\)와 \(\rm\triangle DEF\)가 서로 닮았을 때 기호로

\[\rm\triangle ABC\,\backsim\,\triangle DEF\]

와 같이 나타낸다.

이때 두 도형의 꼭짓점은 보통 대응하는 순서대로 쓴다.

▶ 두 닮은 도형에서 대응하는 변의 길이의 비를 그 두 도형의 닮음비라고 한다.

♠ How to... 점 \(\rm O\)의 위치를 바꿔 닮은 두 삼각형을 살핀다. 슬라이드 \(d\)를 이용하여 비율을 조절한다. 점 \(\rm A,~B,~C\)의 위치를 조절하여 삼각형의 모양을 바꾼다.

▶ 평면도형에서 닮음의 성질

두 닮은 평면도형에서

1. 대응하는 변의 길이의 비는 일정하다.

2. 대응하는 각의 크기는 서로 같다.

▶ 입체도형에서 닮음의 성질

두 닮은 입체도형에서

1. 대응하는 모서리의 길이의 비는 일정하다.

2. 대응하는 면은 서로 닮은 도형이다.

 

❦ 삼각형의 닮음조건

❧ 삼각형의 닮음조건

두 삼각형은 다음의 각 경우에 서로 닮은 도형이다.

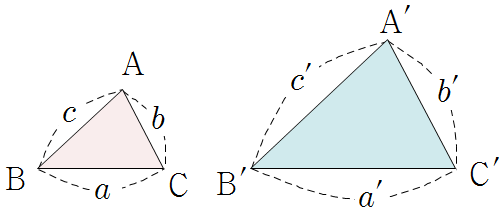
▶ 대응하는 세 쌍의 변의 길이의 비가 각각 같을 때(SSS 닮음)

\(a\,:\,a'=b\,:\,b'=c\,:\,c'\)

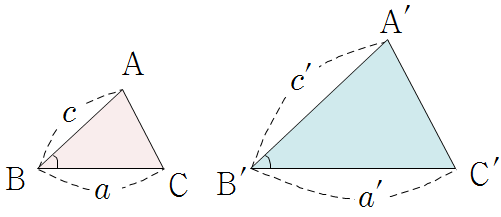
▶ 대응하는 두 쌍의 변의 길이의 비가 각각 같고, 그 끼인 각의 크기가 같을 때(SAS닮음)

\(a\,:\,a'=c\,:\,c',~\rm\angle B=\angle B'\)

▶ 대응하는 두 쌍의 각의 크기가 각각 같을 때(AA닮음)

\(\rm\angle B=\angle B',~\angle C=\angle C'\)

 

❧ 직각삼각형에서의 닮음

다음과 같이 \(\rm\angle A=90^\circ\)인 직각삼각형 \(\rm ABC\)의 꼭짓점 \(\rm A\)에 내린 수선의 발을 \(\rm H\)라고 할 때, 다음이 성립한다.

\[\rm\triangle ABC\,\backsim\,\triangle HBA\]

\[\rm\triangle ABC\,\backsim\,\triangle HAC\]

\[\rm\triangle HBA\,\backsim\,\triangle HAC\]

 

❦ 삼각형과 평행선

❧ 삼각형에서 평행선과 선분의 길이의 비(1)

▶ \(\rm\triangle ABC\)에서 한 직선이 \(\rm\overline {AB}\), \(\rm\overline {AC}\) 또는 그 연장선과 만나는 점을 각각 \(\rm D\), \(\rm E\)라고 할 때

1. \(\rm\overline {BC}\mathrel {/\!/}\rm\overline {DE}\)이면 \(\rm \overline {AB}\,:\,\overline {AD}=\overline {AC}\,:\,\overline {AE}=\overline {BC}\,:\,\overline {DE}\)

2. \(\rm \overline {AB}\,:\,\overline {AD}=\overline {AC}\,:\,\overline {AE}=\overline {BC}\,:\,\overline {DE}\)이면 \(\rm\overline {BC}\mathrel {/\!/}\rm\overline {DE}\)

♠ How to... 점 \(\rm D\)를 끌어 삼각형의 모양에 따른 닮음을 찾도록 한다.

 

▶ \(\rm\triangle ABC\)에서 한 직선이 \(\rm\overline {AB}\), \(\rm\overline {AC}\) 또는 그 연장선과 만나는 점을 각각 \(\rm D\), \(\rm E\)라고 할 때

1. \(\rm\overline {BC}\mathrel {/\!/}\rm\overline {DE}\)이면 \(\rm \overline {AD}\,:\,\overline {DB}=\overline {AE}\,:\,\overline {EC}\)

2. \(\rm \overline {AD}\,:\,\overline {DB}=\overline {AE}\,:\,\overline {EC}\)이면 \(\rm\overline {BC}\mathrel {/\!/}\rm\overline {DE}\)