❦ 평행사변형의 성질
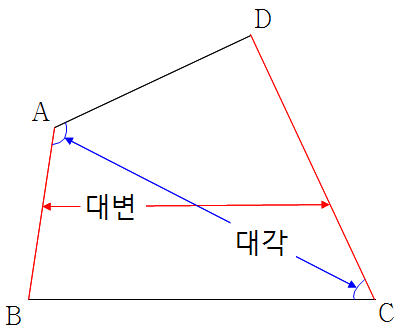
❧ 사각형 \(\rm ABCD\) : \(□\rm ABCD\)
|
|
\(\angle\rm A\)의 대각은 각 \(\angle\rm C\) \(\rm \overline {AB}\)의 대변은 \(\rm \overline {CD}\) |
❧ 평행사변형의 성질
\(평행사변형이면 \begin {cases}(1)~두~쌍의~대변의~길이가~각각~같다.\\(2)~두~쌍의~대각의~크기가~각각~같다.\\(3)~두~대각선은~서로~다른~것을~이등분한다.\end {cases}\)
|
♠ How to...
|
❧ 평행사변형이 되는 조건
\(\left.\begin {aligned}&(1)~두~쌍의 ~대변이~각각~평행하면\\&(2)~두~쌍의~대변의~길이가 ~각각~같으면\\&(3)~두~쌍의~대각의~크기가~각각~같으면\\&(4)~두~대각선이~서로~다른~것을~이등분하면\\&(5)~한~쌍의~대변이~평행하고,~그~길이가~같으면\end {aligned}\qquad\qquad\qquad\right\}평행사변형이다.\)
|
♠ How to...
|
❦ 여러 가지 사각형의 성질
❧ 직사각형
▶ 직사각형은 네 각의 크기가 같은 사각형이다.
▶ 직사각형은 두 쌍의 대각의 크기가 각각 같으므로 평행사변형의 성질을 만족한다.
▶ 직사각형의 두 대각선의 길이는 같고, 서로 다른 것을 이등분한다.
|
♠ How to...
|

† 두 대각선의 길이가 같은 사각형을 직사각형이라고 할 수는 없다.

❧ 마름모
▶ 마름모는 네 변의 길이가 같은 사각형이다.
▶ 마름모는 두 쌍의 대 변의 길이가 각각 같으므로 평행사변형의 성질을 만족한다.
▶ 마름모의 두 대각선은 서로 다른 것을 수직이등분한다.
|
♠ How to...
|

† 두 대각선이 서로 직교한다고 마름모라고 할 수는 없다.
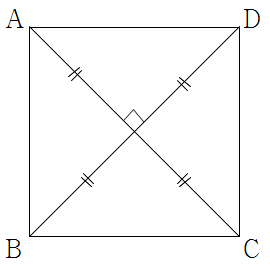
❧ 정사각형
▶ 정사각형은 네변의 길이가 같고 네 내각의 크기가 같은 사각형이다.
▶ 정사각형은 네 변의 길이가 같으므로 마름모이고, 네 내각의 크기가 같으므로 직사각형이다.
▶ 정사각형의 두 대각선은 길이가 같고, 서로 다른 것을 수직이등분한다.
❧ 등변사다리꼴
▶ 사다리꼴은 한 쌍의 대변이 평행한 사각형이다.
▶ 사다리꼴 중에서 아랫변의 양 끝각의 크기가 같은 사다리꼴을 등변사다리꼴이라고 한다.
▶ 등변사다리꼴의 평행하지 않은 한 쌍의 대변의 길이는 같다.
▶ 등변사다리꼴의 두 대각선의 길이는 서로 같다.
|
♠ How to...
|
❧ 여러 가지 사각형 사이의 관계

❦ 평행선과 넓이 사이의 관계
❧ 평행선의 성질을 이용하여 어떤 다각형을 넓이는 변하지 않으면서 모양이 다른 도형으로 바꿀 수 있다.
|
♠ How to...
|
|
|
♠ How to...
|
☞ 한 걸음 더
-
quadrilateral(quadrangle, tetragon) : 사각형
-
parallelogram : 평행사변형
-
rhombus(rhomb) : 마름모
-
rhomboid : 내각의 크기가 \(90^\circ\)가 아닌 평행사변형
-
rectangle : 직사각형
-
square(regular quadrilateral) : 정사각형
-
oblong : 정사각형이 아닌 직사각형
-
kite : 두 쌍의 이웃한 변의 길이가 각각 같고, 대각선이 직교하는 사각형(연꼴)
-
right kite : 한 쌍의 대각의 크기가 \(90^\circ\)인 연꼴
-
trapezium : 대변이 평행하지 않은 사각형
-
trapezoid : 사다리꼴
-
isosceles trapezoid : 등변사다리꼴
-
tangential trapezoid : 내접원을 갖는 사다리꼴
-
tangential quadrilateral : 내접원을 갖는 사각형
-
cyclic quadrilateral : 외접원을 갖는 사각형
-
bicentric quadrilateral : 내접원과 외접원을 갖는 사각형
-
orthodiagonal quadrilateral : 대각선이 직교하는 사각형
-
equidiagonal quadrilateral : 대각선의 길이가 같은 사각형
-
ex-tangential quadrilateral : 네 변의 연장선에 모두 접하는 원이 존재하는 사각형
♠ 넓이의 변화가 없는 도형
- 점 \(\rm H\)를 잡고 정사각형을 회전시킬때 초록색 도형의 넓이는 변화가 없음을 설명한다.
|
♠ How to... |
♠ 한 쌍의 대각과 한 쌍의 대변이 같을 때 평행사변형이 안되는 예
- 점 \(\rm D\)를 끌어 두 사각형을 비교한다.
- 점 \(\rm Q\)를 끌어 삼각형과 사각형을 비교한다.
|
♠ How to... |
Copyright © 2003-2017 trsketch. All Rights Reserved. trsketch.dothome.co.kr
Saturday, July 18, 2015