확률

✾ 확률

❦ 확률의 뜻

❧ 확률 : 같은 조건에서 실험이나 관찰을 여러 번 반복할 때, 반복 횟수가 많아짐에 따라 어떤 사건 $A$ 가 일어나는 상대도수가 일정한 값에 가까워지면 이 일정한 값을 사건 $A$ 가 일어날 확률이라고 한다.

❧ 일반적으로 어떤 실험이나 관찰에서 각 경우가 일어날 가능성이 같을 때, 일어날 수 있는 모든 경우의 수를 $n$ , 사건 $A$ 가 일어날 경우의 수를 $a$ 라고 하면 사건 $A$ 가 일어날 확률 $p$ 는 $p=\dfrac { (사건~A가~일어날~경우의~수)} { (일어날~수~있는~모든~경우의~수)}=\dfrac {a}{n}$ 이다.

예) 동전 한 개를 던질 때 앞면과 뒷면이 나올 가능성이 같다고 볼 수 있으므로 동전의 앞면이 나올 확률은 $\dfrac12$ 이다.

❦ 확률의 성질

❧ 확률의 성질(1)

(1) 어떤 사건이 일어날 확률을 $p$ 라고 하면 $0\leq p\leq1$ 이다.

(2) 절대로 일어나지 않는 사건의 확률은 $0$ 이다.

(3) 반드시 일어나는 사건의 확률은 $1$ 이다.

예) 주사위 한 개를 던질 때,

1) $6$ 이하의 자연수가 나올 확률은 $1$ 이다.

2) 음수가 나올 확률은 $0$ 이다.

❧ 확률의 성질(2)

사건 $A$ 가 일어날 확률을 $p$ 라고 하면, 사건 $A$ 가 일어나지 않을 확률은 $1-p$ 이다.

예) 동전 $2$ 개를 동시에 던질 때, 모두 앞면이 나올 확률은 $\dfrac14$ 이므로 적어도 한 개가 뒷면이 나올 확률은 $1-\dfrac14=\dfrac34$ 이다.

❦ 확률의 계산

❧ 두 사건 $A,~B$ 가 동시에 일어나지 않을 때, 사건 $A$ 가 일어날 확률을 $p$ , 사건 $B$ 가 일어날 확률을 $q$ 라고 하면 사건 $A$ 또는 사건 $B$ 가 일어날 확률은 $p+q$ 이다.

예) 서로 다른 두 개의 주사위를 동시에 던질 때, 나오는 눈의 수의 합이 $3$ 또는 $12$ 가 될 확률을 구하여라.

눈의 수의 합이 $3$ 일 확률이 $\dfrac { 2} { 36}$ 이고, 눈의 수의 합이 $12$ 일 확률이 $\dfrac { 1} { 36}$ 이므로 눈의 수의 합이 $3$ 또는 $12$ 가 될 확률은

$\frac { 2} { 36}+\frac { 1} { 36}=\frac { 1} { 12}$

이다.

❧ 두 사건 $A,~B$ 가 서로 영향을 끼치지 않을 때, 사건 $A$ 가 일어날 확률을 $p$ , 사건 $B$ 가 일어날 확률을 $q$ 라고 하면 사건 $A$ 와 사건 $B$ 가 동시에 일어날 확률은 $p\times q$ 이다.

예) 동전 $1$ 개와 주사위 $1$ 개를 동시에 던질 때, 동전은 앞면이 나오고 주사위는 짝수의 눈이 나올 확률을 구하여라.

동전의 앞면이 나올 확률은 $\dfrac12$ 이고, 주사위가 짝수의 눈이 나올 확률은 $\dfrac36$ 이므로 동전은 앞면이 나오고 주사위는 짝수의 눈이 나올 확률은

$\frac12\times\frac36=\frac14$

이다.

☞ 한 걸음 더

♠ 확률 실험

동전 한 개를 여러 번 던질 때 동전의 앞면이 나오는 비율을 시뮬레이션해보자.

♠ 여러 가지 확률 문제

같은 능력을 가진 두 사람 $A,~B$ 가 같은 금액의 돈을 각각 걸고 경기를 하고 있다. 먼저 $3$ 번 이긴 사람이 돈을 모두 가져가기로 했는데 $A$ 가 두 번 이기고, $B$ 가 한 번 이긴 상황에서 경기가 중지되었다. 돈을 공평하게 나눌 수 있는 방법은 무엇인가?
당신이 게임 쇼에 출연하여 세 개의 문들 중에서 하나를 선택하라는 요구를 받았다. 이들 중 하나의 문 뒤에는 고급 자동차가 있고 다른 두 개의 문 뒤에는 염소가 앉아 있다. 당신이 한 개의 문을 선택하자, 모든 상황을 이미 알고 있는 사회자가 다른 문을 열어 보였다. 거기에는 염소가 앉아 있다. 사회자는 익살맞은 표정으로 당신에게 묻는다. "다른 문으로 선택을 바꾸셔도 됩니다. 지금 바꾸시겠습니까?" 이 상황에서 당신은 어떤 선택을 내려야 할까?
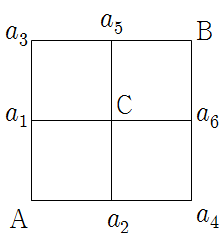
점 $\rm A$ 에서 점 $\rm C$ 를 거쳐 점 $\rm B$ 로 가는 최단거리의 길을 선택할 확률은?

	→ → ↑ ↑	그림과 같은 블록의 도로망이 있을 때, 최단거리의 경우의 수는 총 $6$ 가지이다. 이 중에서 점 $\rm C$ 를 거쳐가는 경우는 $4$ 가지이다. 따라서 점 $\rm C$ 를 거쳐가는 최단거리를 선택할 확률은 $\frac23$ 이다. 정말 확률이 $\frac23$ 일까?
	↑ ↑ → →
	→ ↑ → ↑
	→ ↑ ↑ →
	↑ → ↑ →
	↑ → → ↑

☞ 이렇게 생각해보자. 점 $\rm A$ 에서 갈림길이 있으므로 우선 하나의 길을 선택할 확률은 $\frac12$ 이다. 그 다음에 $a_1$ 혹은 $a_2$ 지점에 도달하면 다시 각각의 갈림길에서 하나의 길을 선택할 확률이 $\frac12$ 이 된다. 만일 $a_3$ 나 $a_4$ 지점을 선택한다면 이후에는 선택할 필요가 없어지므로 $a_1$ 에서 $a_3$ 를 지나 $\rm B$ 로 가는 길과 $a_2$ 에서 $a_4$ 를 지나 $\rm B$ 로 가는 길을 선택할 확률은 각각 $\frac12 \times\frac12 = \frac14$ 이다. 반면 $\rm C$ 를 선택하게 된다면 여기에서 다시 $a_5$ 나 $a_6$ 를 선택해야하므로 이때의 $4$ 가지 경우는 모두 각각 $\frac12\times\frac12\times\frac12 =\frac18$ 의 확률을 갖는다. 따라서 점 $\rm A$ 에서 점 $\rm C$ 를 거쳐 점 $\rm B$ 로 가는 최단거리의 길을 선택할 확률은 $\frac12$ 이다. 이 결과는 주사위를 던져서 각각의 눈의 나올 확률이 $\frac16$ 이라는 것과 이 문제는 근본적으로 서로 다르다는 것을 얘기해준다. 이 문제는 확률의 동등성의 원리(equally likely)에 맞지 않기 때문에 처음의 방법으로 해결하면 안되는 것이다.

Home

교육과정

중학수학

MathJax

gadgets

chronicle

Favorites

tistory1

tistory2