❦ 미지수가 \(2\)개인 일차방정식의 그래프와 일차함수의 그래프

❧ 직선의 방정식 : 일반적으로 \(x,~y\)의 값이 수 전체일 때, 일차방정식

\[ax+by+c=0\,(a,~b,~c는~상수,~a\neq 0~ 또는~b\neq 0)\]

의 해는 무수히 많고, 그 해를 좌표평면 위에 나타내면 직선이 된다. 또, 이 직선 위의 모든 점의 좌표는 일차방정식 \(ax+by+c=0\)의 해이다. 이 일차방정식을 직선의 방정식이라고 한다.

 

❧ 미지수가 \(2\)개인 일차방정식의 그래프와 일차함수의 그래프

미지수가 \(2\)개인 일차방정식

\[ax+by+c=0\,(a,~b,~c는~상수,~a\neq 0,~b\neq 0)\]

의 그래프는 일차함수

\[y=-\dfrac {a} {b}x-\dfrac {c} {b}\]

의 그래프와 같다.

예) 일차방정식 \(2x+3y-1=0\)의 그래프는 일차함수 \(y=-\dfrac 23 x+\dfrac13\)의 그래프와 같다.

 

❦ 일차방정식 \(x=p,~y=q\)의 그래프

❧ \(x=p\)(\(p\)는 상수)의 그래프

  (1) 점 \((p,~0)\)을 지나고, \(y\)축에 평행한 직선이다.

  (2) \(x=0\)의 그래프는 \(y\)축과 일치한다.

 

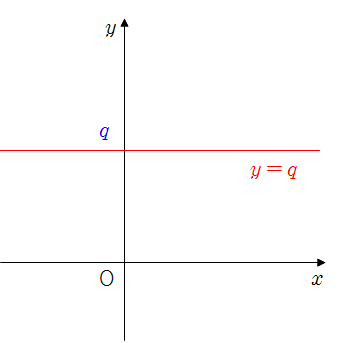
❧ \(y=q\)(\(q\)는 상수)의 그래프

  (1) 점 \((0,~q)\)를 지나고, \(x\)축에 평행한 직선이다.

  (2) \(y=0\)의 그래프는 \(x\)축과 일치한다.

 

    

 

❦ 연립방정식의 해와 일차함수의 그래프

❧ 연립방정식의 해와 그래프

연립방정식

\[\begin {cases}ax+by=c \\a'x+b'y=c'  \end {cases} ~(a\neq0,~b\neq0,~a'\neq0,~b'\neq0)\]

의 해는 두 일차함수

\[y=-\dfrac ab x+ \dfrac cb ,~y=- \dfrac {a'} {b'}x+\dfrac {c'} {b'}\]

의 그래프의 교점의 좌표와 같다.

 

❧ 연립방정식의 해와 그래프의 위치 관계

연립방정식에서 각 방정식의 그래프인 두 직선이

  (1) 한 점에서 만나면 해는 하나이다.

  (2) 일치하면 해는 무수히 많다.

  (3) 평행하면 해가 없다.

 

♠ How to... 슬라이드 \(a,~b,~c\)를 이용하여 \(ax+by=c\)의 \(a,~b,~c\)의 값에 변화를 줘 본다. 슬라이드 \(d,~e,~f\)를 이용하여 \(dx+ey=f\)의 \(d,~e,~f\)의 값에 변화를 줘 본다. 두 그래프의 교점의 좌표를 관찰한다.