❦ 일차함수의 뜻

❧ 일차함수 : 함수 \(y=f(x)\)에서\[y=ax+b\,(a,~b는~상수,~a\neq0)\]와 같이 \(y\)가 \(x\)에 관한 일차식으로 나타내어질 때, 이 함수를 \(x\)에 관한 일차함수라고 한다.

예) \(y=2x+1,~y=-x+3,~y=\dfrac x4+3\)

 

❦ 일차함수 \(y=ax+b\)의 그래프

❧ 일차함수의 그래프

\(y=\)\(x+\)      

 

♠ How to... 점 \(\rm A\)를 드래그하여 점 \(\rm P\)의 위치 변화를 확인한다. 슬라이드 \(a,~b\)를 이용하여 \(y=ax+b\)의 \(a,~b\)의 값에 변화를 줘 본다. 점 \(\rm P\)를 마우스 우클릭하여 [자취 보이기]를 활성시키고 점 \(\rm A\)를 드래그 해본다. 점 \(\rm A\)를 마우스 우클릭하여 [애니메이션 시작]을 활성시키면 함수의 그래프를 볼 수 있다. 체크박스를 통하여 완전한 그래프를 확인할 수 있다. 우측 상단의 '새로 고침' 버튼을 통해 초기화 시킬 수 있다.

 

❧ 평행이동 : 한 도형을 일정한 방향으로 일정한 거리만큼 옮기는 것

▶ 일차함수 \(y=ax+b\)의 그래프는 일차함수 \(y=ax\)의 그래프를 \(y\)축의 방향으로 \(b\)만큼 평행이동한 직선이다.

♠ How to... 슬라이드 \(b\)를 이용하여 \(y=ax+b\)의 \(b\)의 값에 변화를 줘 본다. 슬라이드 \(a\)를 이용하여 \(y=ax+b\)의 \(a\)의 값에 변화를 주고, \(b\)의 값에 변화를 줘 본다. 우측 상단의 '새로 고침' 버튼을 통해 초기화 시킬 수 있다.

 

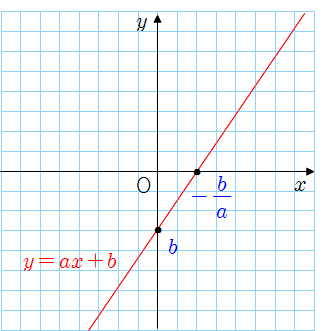
❦ 일차함수의 그래프와 절편

❧ \(x\)절편 : 일차함수 \(y=ax+b\)의 그래프가 \(x\)축과 만나는 점의 \(x\)좌표 ⇒ \(y=0\)일 때의 \(x\)의 값

❧ \(y\)절편 : 일차함수 \(y=ax+b\)의 그래프가 \(y\)축과 만나는 점의 \(y\)좌표 ⇒ \(x=0\)일 때의 \(y\)의 값

▶ 일차함수 \(y=ax+b\)의 그래프가 \(x\)축과 만나는 점의 \(y\)좌표는 \(0\)이므로

\[\begin {aligned}0&=ax+b\\ax&=-b\\x&=-\dfrac {b} {a}\end {aligned}\]

따라서 \(x\)절편은 \(-\dfrac {b} {a}\)이다.

▶ 일차함수 \(y=ax+b\)의 그래프가 \(y\)축과 만나는 점의 \(x\)좌표는 \(0\)이므로

\[\begin {aligned}y&=a\times0+b\\&=b\end {aligned}\]

따라서 \(y\)절편은 \(b\)이다.

 

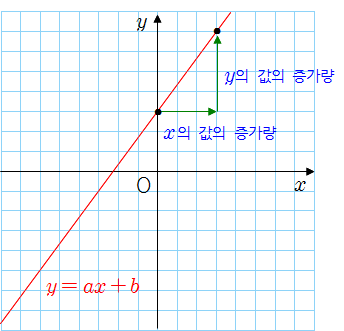
❦ 일차함수의 그래프와 기울기

❧ 일차함수 \(y=ax+b\)의 그래프에서

\[(기울기)=\dfrac { (y의~값의~증가량)} { (x의~값의~증가량)}=a\]

▶ \(y=2x+1\)에 대하여

\(x\)	\(\cdots\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(\cdots\)
\(y\)	\(\cdots\)	\(-3\)	\(-1\)	\(1\)	\(3\)	\(5\)	\(\cdots\)

표에서 \(x\)의 값이 \(1\)만큼 증가하면 \(y\)의 값은 \(2\)만큼 증가하고, \(x\)의 값이 \(2\)만큼 증가하면 \(y\)의 값은 \(4\)만큼 증가한다. 따라서 \(x\)의 값의 증가량에 대한 \(y\)의 값의 증가량의 비율이 \(2\)로 일정함을 알 수 있다.

 

❦ 일차함수의 특징을 이용하여 그래프 그리기

❧ 평행이동을 이용하여 \(y=ax+b\)의 그래프 그리기

(1) \(y=ax\)의 그래프를 그린다.

(2) \(y=ax\)의 그래프의 각 점을 \(y\)축의 방향으로 \(b\)만큼 평행이동한 후, 직선으로 연결한다.

 

❧ 절편을 이용하여 \(y=ax+b\)의 그래프 그리기

(1) \(y=ax+b\)의 \(x\)절편, \(y\)절편을 각각 구한다.

(2) 두 점 \((x절편,~0),~(0,~y절편)\)을 좌표평면 위에 나타낸 후, 직선으로 연결한다.

 

❧ 기울기를 이용하여 \(y=ax+b\)의 그래프 그리기

(1) \((0,~y절편)\)을 좌표평면 위에 나타낸다.

(2) (1)에서 찍은 점으로부터 \(x\)축 방향으로 \(1\)만큼, \(y\)축 방향으로 \(a\)만큼 이동한 점을 찍은 후, 직선으로 연결한다.

 

❦ 일차함수의 그래프의 성질

❧ 일차함수 \(y=ax+b\)의 그래프는

\(a>0\)이면	\(a<0\)이면
오른쪽 위로 향하는 직선이다.	오른쪽 아래로 향하는 직선이다.

 

❧ 일차함수의 그래프의 기울기와 평행

   (1) 기울기가 같은 두 일차함수의 그래프는 서로 평행하거나 일치한다.

   (2) 서로 평행한 두 일차함수의 그래프의 기울기는 서로 같다.

 

❦ 일차함수의 식 구하기

❧ 기울기와 \(y\)절편이 주어진 경우

   기울기가 \(a\)이고 \(y\)절편이 \(b\)인 직선을 그래프로 하는 일차함수의 식

     ⇒ \(y=ax+b\)

예) 기울기가 \(2\)이고 \(y\)절편이 \(-1\)인 직선을 그래프로 하는 일차함수의 식은 \(y=2x-1\)이다.

 

❧ 기울기와 지나는 한 점이 주어진 경우

   기울기가 \(a\)이고 점 \((p,~q)\)를 지나는 직선을 그래프로 하는 일차함수의 식

     (1) 구하는 식을 \(y=ax+b\)라 놓는다.

     (2) \(y=ax+b\)에 \(x=p,~y=q\)를 대입하여 \(b\)의 값을 구한다.

예) 기울기가 \(3\)이고 점 \((1,~5)\)를 지나는 직선을 그래프로 하는 일차함수의 식을 구하여라.

   (1) 구하는 식을 \(y=3x+b\)라 놓는다.

   (2) \(y=3x+b\)에 \(x=1,~y=5\)를 대입하면 \(5=3+b\)이므로 \(b=2\)이다.

따라서 구하는 식은 \(y=3x+2\)이다.

 

❧ 그래프가 지나는 서로 다른 두 점이 주어진 경우

   두 점 \((p,~q)\), \((r,~s)\)를 지나는 직선을 그래프로 하는 일차함수의 식

     (1) 구하는 식을 \(y=ax+b\)라 놓는다.

     (2) \(x\)의 값의 변화량에 대한 \(y\)의 값의 변화량의 비를 이용하여 \(a\)의 값을 구한다. 즉,

\[a=\dfrac {s-q} {r-p}\]

이다.

     (3) \(y=ax+b\)에 두 점 중 계산하기 편한 좌표를 대입하여 \(b\)의 값을 구한다.

예) 두 점 \((-2,~-1)\), \((1,~5)\)를 지나는 직선을 그래프로 하는 일차함수의 식을 구하여라.

   (1) 구하는 식을 \(y=ax+b\)라 놓는다.

   (2) \(a=\dfrac { 5-(-1)} { 1-(-2)}=2\)

   (3) \(y=2x+b\)에 \(x=1,~y=5\)를 대입하면 \(5=2+b\)이므로 \(b=3\)이다.

따라서 구하는 식은 \(y=2x+3\)이다.