❦ 부등식과 그 해

❧ 부등식 : 부등호 \(>,~<,~\geq,~\leq\)를 사용하여 수 또는 식의 대소 관계를 나타낸 식

▶ \(x<3,~2x+1\geq-2,~3x-1<x+2 \) 등

 

❧ 부등식을 참이 되게 하는 미지수의 값을 그 부등식의 해라고 하며, 부등식의 해를 모두 구하는 것을 부등식을 푼다고 한다.

▶ \(x+1>2\)에서

    \(x=2\)이면 \(2+1>2\)이고 참이므로 \(x=2\)는 해이다.

    \(x=3\)이면 \(3+1>2\)이고 참이므로 \(x=3\)은 해이다.

    \(x=-1\)이면 \(-1+1>2\)이고 거짓이므로 \(x=-1\)은 해가 아니다.

 

❦ 부등식의 성질

❧ 부등식의 양변에 같은 수를 더하거나 양변에서 같은 수를 빼어도 부등호의 방향은 바뀌지 않는다.

▶ \(a<b\)이면 \(a+c<b+c,~a-c<b-c\)

 

❧ 부등식의 양변에 같은 양수를 곱하거나 양변을 같은 양수로 나누어도 부등호의 방향은 바뀌지 않는다.

▶ \(a<b,~c>0이면~ ac<bc,~ \dfrac { a} { c} < \dfrac { b} { c}\)

 

❧ 부등식의 양변에 같은 음수를 곱하거나 양변을 같은 음수로 나누면 부등호의 방향은 바뀐다.

▶ \(a<b,~c<0이면~ ac\color { red} { >}bc,~ \dfrac { a} { c}\color { red} { >}\dfrac { b} { c}\)

 

❦ 일차부등식의 풀이

❧ 일차부등식

부등식의 성질을 이용하여 부등식의 모든 항을 좌변으로 옮겨 정리하였을 때\[(일차식)>0,~(일차식)<0,~(일차식)\geq0,~(일차식)\leq0\]의 꼴로 나타낼 수 있는 부등식을 일차부등식이라고 한다.

 

❧ 부등식의 해는 부등식의 성질을 이용하여 주어진 부등식을

\[x>(수),~x<(수),~x\geq(수),~x\leq(수)\]

중 어느 하나의 꼴로 고쳐서 구한다.

 

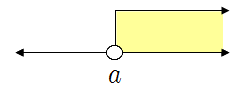
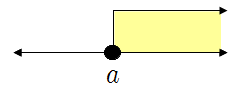
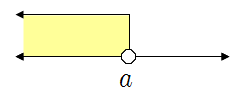
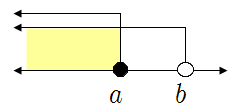
❧ 부등식의 해와 수직선

▶ \(x>a\)	▶ \(x\geq a\)
▶ \(x<a\)	▶ \(x\leq a\)

 

❧ 일차부등식의 풀이

(1) 괄호가 있으면 먼저 괄호를 푼다.

(2) 계수가 분수나 소수이면 적당한 수를 곱하여 계수를 정수로 고친다.

(3) 양변을 정리하여 \(ax<b,~ax>b,~ax\leq b,~ax\geq b~(a\neq0)\)와 같은 모양으로 고친다.

(4) 양변을 \(x\)의 계수로 나눈다.

\(\eqalign {☞ ~x-5&<9-x\\x+x&<9+5\\2x&<14\\x&<7\\\quad }\qquad\eqalign {☞ ~3x+1&\geq4(x+1)\\3x+1&\geq4x+4\\3x-4x&\geq4-1\\-x&\geq3\\x&\leq-3 }\)

 

❦ 연립일차부등식의 풀이

❧ \(\cases{x-1<3\\x+1\geq2}\)와 같이 두 개 이상의 일차부등식을 한 쌍으로 묶어서 나타낸 것을 연립일차부등식 또는 간단히 연립부등식이라고 한다.

 

❧ 연립부등식의 각 부등식을 동시에 만족하는 \(x\)의 값을 그 연립부등식의 해라 하고, 연립부등식의 모든 해를 구하는 것을 연립부등식을 푼다고 한다.

 

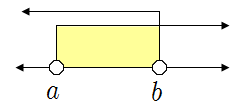
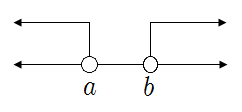
❧ 연립부등식의 해와 수직선

▶ \(a<x<b\)	▶ \(x\geq b\)
▶ \(x\leq a\)	▶ 해가 없다.

 

❧ 연립부등식의 풀이

▶ \(\begin {cases}2x+3>1\quad&\cdots\cdots~①\\3x-1 \geq2x&\cdots\cdots~②\end {cases}\)

부등식 ①을 풀면 \(x>-1\)

부등식 ②를 풀면 \(x\geq1\)

두 부등식 ①, ②의 해를 수직선 위에 함께 나타내면 다음과 같다.

따라서 구하는 해는 \(x\geq1\)이다.

 

❧ 복잡한 연립부등식의 풀이

▶ 괄호가 있는 식은 괄호를 풀어 정리하고 연립한다.

▶ 계수가 소수나 분수이면 양변에 적당한 수를 곱하여 계수가 정수가 되도록 만들어 정리하고 연립한다.

▶ \(A<B<C\)형태는 \(\cases {A<B\\B<C}\)로 고쳐서 푼다.

 

 

❦ 부등식의 활용

❧ 부등식을 이용하여 문제를 해결하는 순서

(1) 문제의 뜻을 파악하고, 무엇을 미지수로 놓을지 결정한다.

(2) 수량들 사이의 대소 관계를 일차부등식으로 나타낸다.

(3) 부등식을 푼다.

(4) 구한 해가 문제의 뜻에 맞는지 확인한다.

▶ 밑변의 길이가 \(x\,\rm cm\), 높이가 \(8\,\rm cm\)인 삼각형이 있다. 이 삼각형의 넓이가 \(20\,\rm cm^2\) 이상 \(28\,\rm cm^2\) 이하가 되게 하려 할 때, 이 삼각형의 밑변의 길이의 범위를 구하여라.

\(\begin {gathered}20\leq \dfrac12 \times8\times x \leq28\\20\leq4x \leq28\\5\leq x\leq7 \end {gathered}\)