❦ 다항식의 덧셈과 뺄셈

❧ 분배법칙을 이용하여 괄호를 풀고, 동류항끼리 모아서 간단히 한다.

 

\( \begin {aligned}예) (3x+2y)+(4x-3y)&=3x+2y+4x-3y\\&=3x+4x+2y-3y\\&=7x-y\end {aligned}\)

 

\( \begin {aligned}예) (3x+2y)-(4x-3y)&=3x+2y-4x+3y\\&=3x-4x+2y+3y\\&=-x+5y\end {aligned}\)

 

❧ 이차식

▶ 다항식의 각 항의 차수 중 가장 높은 차수가 2인 다항식

  예) \(x^2+2x+1,\quad 3x^2-x+4,\quad 4x^2\)

 

▶ 이차식의 덧셈과 뺄셈 : 일차식과 마찬가지로 먼저 괄호를 풀고 동류항끼리 모아서 간단히 한다.

    \(\begin {aligned}예)~~~&(x^2-2x+3)-(2x^2+3x-1)\\=&\;x^2-2x+3-2x^2-3x+1\\=&-x^2-5x+4\end {aligned}\)

 

❦ 다항식의 곱셈과 나눗셈

❧ \((단항식)\times(다항식)\) : 분배법칙을 이용하여 다음과 같이 계산한다.

\[2x(a+b)=2x\times a+2x \times b\]

 

❧ 전개 : 단항식과 다항식의 곱셈에서 분배법칙을 이용하여 하나의 다항식으로 나타내는 것

\[2a(x+3y)\xrightarrow[전개] {}2ax+6ay \]

 

❧ \((다항식)\div(단항식)\) : 역수를 이용하거나, 분수식으로 바꾸어 계산한다.

【방법1】역수이용 \(\begin {aligned}(A+B)\div C &=(A+B)\times\displaystyle {\frac { 1} { C}} \\&=\displaystyle { \frac { A} { C}+\frac { B} { C}}\end {aligned}\)

【방법2】분수꼴로 \(\begin {aligned}(A+B)\div C &=\displaystyle { \frac { A+B} { C}} \\&=\displaystyle { \frac { A} { C}+\frac { B} { C}}\end {aligned}\)

예)

\(\begin {aligned}(6a^2+2a)\div2a &=(6a^2+2a)\times\displaystyle { \frac { 1} { 2a}} \\&=6a^2\times\displaystyle {\frac { 1} { 2a}}+2a\times\displaystyle { \frac { 1} { 2a}} \\&=3a+1\end {aligned}\)

 

\(\begin {aligned}(6a^2+2a)\div2a &=\displaystyle { \frac { 6a^2+2a} { 2a}} \\&=3a+1\end {aligned}\)

 

❦ \((다항식)\times(다항식)\)

❧ 다항식과 다항식의 곱셈은 단항식과 다항식의 곱셈과 마찬가지로 분배법칙을 이용하여 전개한다.

 

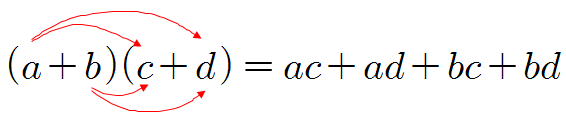
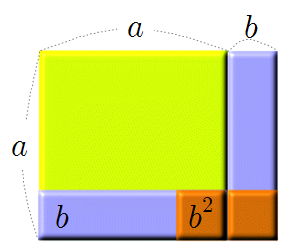
❦ 곱셈공식

❧ \((a+b)^2=a^2+2ab+b^2, \quad (a-b)^2=a^2-2ab+b^2\)

\(\begin{aligned}(a+b)^2&=(a+b)(a+b)\\&=a^2+ab+ab+b^2\\&=a^2+2ab+b^2\end{aligned}\)
\(\begin{aligned}(a-b)^2&=(a-b)(a-b)\\&=a^2-ab-ab+b^2\\&=a^2-2ab+b^2\end{aligned}\)

 

❧ \((a+b)(a-b)=a^2-b^2\)

\(\begin {aligned}(a+b)(a-b)&=a^2-ab+ab-b^2\\&=a^2-b^2\end {aligned}\)

 

❧ \((x+a)(x+b)=x^2+(a+b)x+ab\)

 

\(\begin {aligned}(x+a)(x+b)&=x^2+ax+bx+ab\\&=x^2+(a+b)x+ab\end {aligned}\)

 

 

❧ \((ax+b)(cx+d)=acx^2+(ad+bc)x+bd\)

 

\(\begin{aligned}(ax+b)(cx+d)&=acx^2+adx+bcx+bd\\&=acx^2+(ad+bc)x+bd\end{aligned}\)

 

❧ 곱셈공식의 활용

▶ \((x+a)^2, (x-a)^2\)을 이용한 계산

  예) \(101^2=(100+1)^2=100^2+2\times 100+1=10201\)

 

▶ \((a+b)(a-b)\)를 이용한 계산

  예) \(101\times99=(100+1)(100-1)=100^2-1=9999\)

 

 

❦ 등식의 변형

❧ 주어진 식의 문자에 그 문자를 나타내는 다른 식을 대입하여 주어진 식을 변형할 수 있다.

 

예) \(y=x+1\)일 때, \(2y+1\)에 대입하면 \(2(x+1)+1=2x+3\)으로 나타내어진다. 이것은 \(y\)의 식 \(2y+1\)을 \(x\)의 식 \(2x+3\)으로 변형한 것이다.

 

❧ 문자를 포함한 등식에서 한 문자를 다른 문자의 식으로 변형하여 나타낼 수 있다.

 

예) \(2x+y=3\)일 때, \(y\)를 \(x\)의 식으로 나타내면 \(y=-2x+3\)이다. 이것을 '\(y\)에 관하여 풀었다'고 한다.

 

❧ 곱셈공식의 변형

▶ \((a+b)^2=a^2+2ab+b^2\)이므로

\[a^2+b^2=(a+b)^2-2ab\]

 

▶ \((a-b)^2=a^2-2ab+b^2\)이므로

\[a^2+b^2=(a-b)^2+2ab\]

 

▶ \(\displaystyle {\left(x+\frac 1 {x}\right)^2=x^2+\frac 1 {x^2}+2}\)이므로

\[\displaystyle {x^2+\frac 1 {x^2}=\left(x+\frac 1 {x}\right)^2-2}\]

 

▶ \(\displaystyle {\left(x-\frac 1 {x}\right)^2=x^2+\frac 1 {x^2}-2}\)이므로

\[\displaystyle {x^2+\frac 1 {x^2}=\left(x-\frac 1 {x}\right)^2+2}\]