❦ 유리수와 소수
❧ 유리수 : 두 정수 \(a, b\)에 대하여 \(\dfrac ab (b\neq 0)\)인 꼴로 나타낼 수 있는 수
❧ 소수
▶ 유한소수 : 소수점 아래의 \(0\)이 아닌 숫자가 유한 개인 소수
예) \( 0.5,\enspace 0.12,\enspace 2.15,\enspace \cdots \)
▶ 무한소수 : 소수점 아래의 \(0\)이 아닌 숫자가 무수히 많은 소수
예) \(0.333\cdots ,\enspace 0.666\cdots ,\enspace \pi = 3.141592\cdots ,\enspace \cdots \)
❧ 유한소수로 나타낼 수 있는 분수
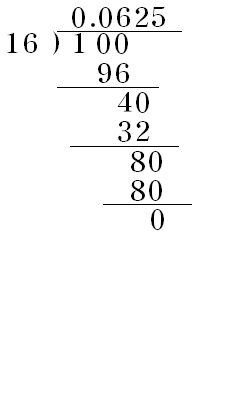
▶ 모든 유한소수는 분모가 \(10\)의 거듭제곱 꼴인 분수로 나타낼 수 있다.
예) \( 0.3= \dfrac { 3}{ 10} , 0.2= \dfrac { 2}{ 10} = \dfrac { 1}{ 5} , 0.25 = \dfrac { 25}{ 100}= \dfrac { 1}{ 4} \)
▶ 기약분수의 분모의 소인수가 \(2\)나 \(5\)뿐이면 유한소수로 나타낼 수 있다.
예) \( \dfrac { 3}{ 20}=\dfrac { 3}{ 2^2 \times 5}\left( = \dfrac { 15}{ 100}\right)\)
\( \dfrac { 7}{ 50}=\dfrac { 7}{ 2 \times 5^2}\left( = \dfrac { 14}{ 100}\right)\)
\( \dfrac { 1}{ 60}=\dfrac { 1}{ 2^2 \times3 \times 5}\left( = 0.01666 \cdots \right)\) \(\Rightarrow\) 무한소수

† 우리가 사용하는 수는 십진법으로 나타낸 것이다. 십진법은 \(10\)의 거듭제곱을 이용하여 각 자리의 수를 표현하는데 \(10=2\times5\)이다. 한편 소수점 아래의 자리는 \(1\over10\), \(1\over8\), \(\frac19 \cdots\)으로 \(10\)의 거듭제곱의 역수이다. 따라서 유한소수로 나타낼 수 있는 분수는 모두 분모, 분자에 적당한 수를 곱하여 분모를 \(10\)의 거듭제곱으로 나타낼 수 있다.
❦ 순환소수
❧ 순환소수 : 소수점 아래의 어떤 자리에서부터 한 숫자 또는 몇 개의 숫자의 배열이 한없이 되풀이되는 무한소수
▶ 예) \(0.111\cdots, \enspace0.1212\cdots, \enspace2.3535\cdots, \enspace0.08282\cdots\)
❧ 순환마디 : 순환소수의 소수점 아래에서 일정하게 되풀이되는 부분
❧ 순환소수의 표현 : 순환마디의 양 끝의 숫자 위에 점을 찍어서 간단히 나타낸다.
|
순환소수 |
순환마디 |
표현 |
|
\(0.3333\cdots\) |
\(3\) |
\(0.\dot3\) |
|
\(0.272727\cdots\) |
\(27\) |
\(0.\dot2\dot7\) |
|
\(0.03434\cdots\) |
\(34\) |
\(0.0\dot3\dot4\) |
|
\(3.153153153\cdots\) |
\(153\) |
\(3.\dot1 5\dot3\) |
❧ 순환소수로 나타낼 수 있는 분수
분모를 기약분수로 나타내었을 때, 분모에 \(2\) 또는 \(5\) 이외의 소인수가 있으면 그 분수는 무한소수가 되며, 그 무한소수는 순환소수로 나타내어진다.

❧ 소수와 유리수


† \(0.\dot3 ,\enspace0.\dot3\dot3 ,\enspace0.\dot3 3\dot3 \)은 모두 풀어쓰면 \(0.3333\cdots\)을 나타낸다. 그럼 순환마디를 무엇이라고 해야 할까? 혼동을 피하고 가장 간단하게 표현하는 경우는 \(0.\dot3\)이므로 \(0.333\cdots\)의 순환마디는 \(3\)이다. 즉, 가장 간단하게 표현할 경우를 고려하여 순환마디를 정하도록 한다.
❦ 순환소수를 분수로 나타내기
❧ 방정식 이용하기
|
(1) 주어진 순환소수를 \(x\)라 놓는다. (2) 소수점 아래의 숫자의 배열이 같아지도록 \(10\)의 거듭제곱을 곱한다. (3) (2)에서 구한 두 식을 변끼리 뺀다. (4) 등식의 성질을 이용하여 \(x\)를 구한다. |
\(x=0.232323\cdots\)이라면 \(\qquad\enspace 100x=23.2323\cdots\) \(-\underline {)\qquad\quad x=\enspace 0.2323\cdots}\) \(\quad100x-x=23\) \(\qquad\qquad\enspace x=\dfrac { 23}{ 99}\) |
❧ 공식 이용하기
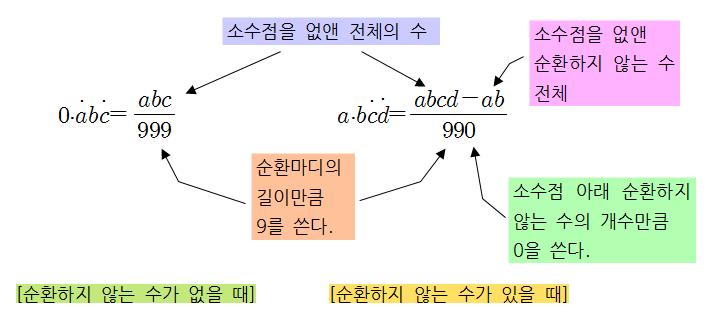
☞ 한 걸음 더
♠ 순환마디 관찰하기
♠ \(0.999\cdots=1\) !?
|
\(\dfrac { 1}{ 3}=0.3333\cdots\)의 양변에 \(3\)을 곱하면 \(3\times \dfrac13=3\times0.3333\cdots\) \(\qquad \: 1=0.9999\cdots\) |
\(\enspace\:\: x=0.9999\cdots\) …… ㉠ \(10x=9.9999\cdots\) …… ㉡ ㉡-㉠을 계산하면 \(10x-x=9\) \(\therefore x= \dfrac99=1\) |
Copyright © 2003-2017 trsketch. All Rights Reserved. trsketch.dothome.co.kr
Saturday, July 18, 2015