❦ 기둥의 겉넓이와 부피
❧ 기둥의 겉넓이 : 전개도를 이용하여 두 밑넓이와 옆넓이의 합으로 구할 수 있다.
\[(기둥의~겉넓이)=(밑넓이)\times2+(옆넓이)\]
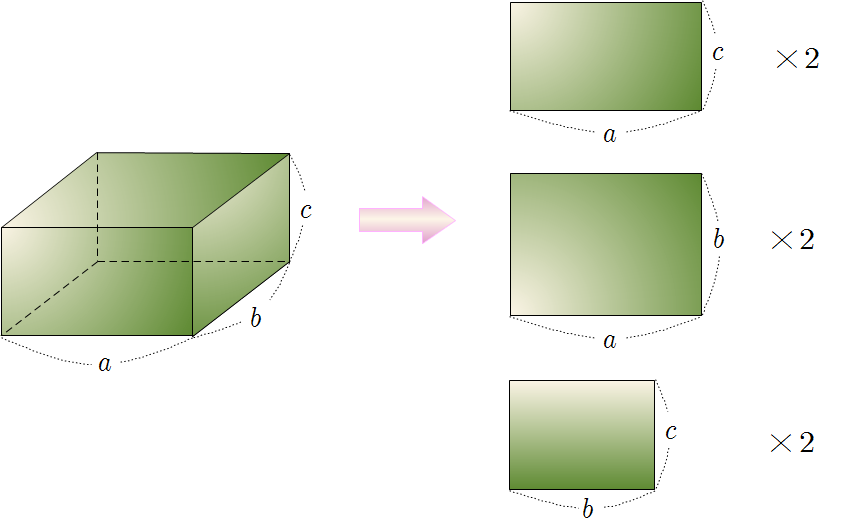

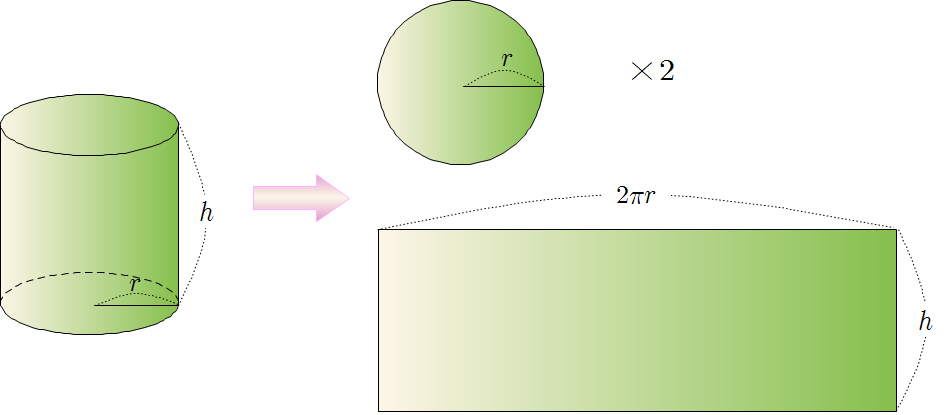
❧ 기둥의 부피
\[(기둥의~부피)=(밑넓이)\times(높이)\]
❦ 뿔의 겉넓이와 부피
❧ 뿔의 겉넓이 : 전개도를 이용하여 밑넓이와 옆넓이의 합으로 구할 수 있다.
\[(뿔의~겉넓이)=(밑넓이)+(옆넓이)\]

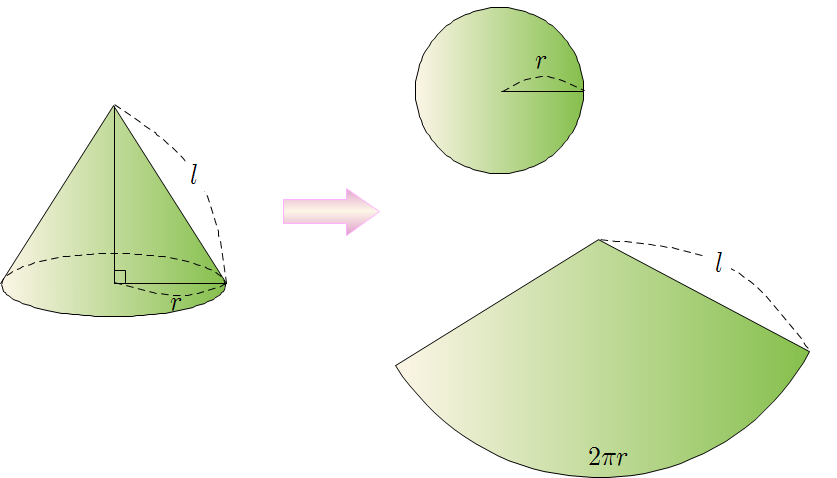
❧ 뿔의 부피
\[(뿔의~부피)=\frac13\times(밑넓이)\times(높이)\]
❧ 각뿔대, 원뿔대의 겉넓이와 부피
▸ 각뿔대, 원뿔대의 겉넓이 : 전개도를 이용하여 두 밑넓이와 옆넓이의 합으로 구할 수 있다.
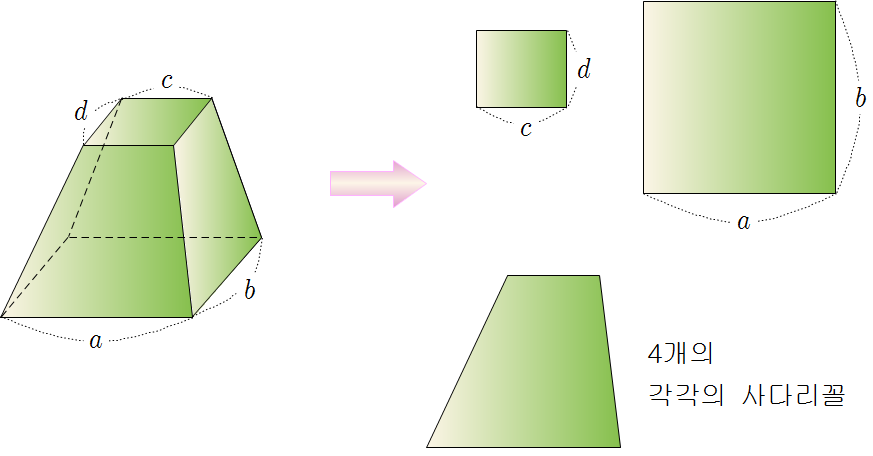
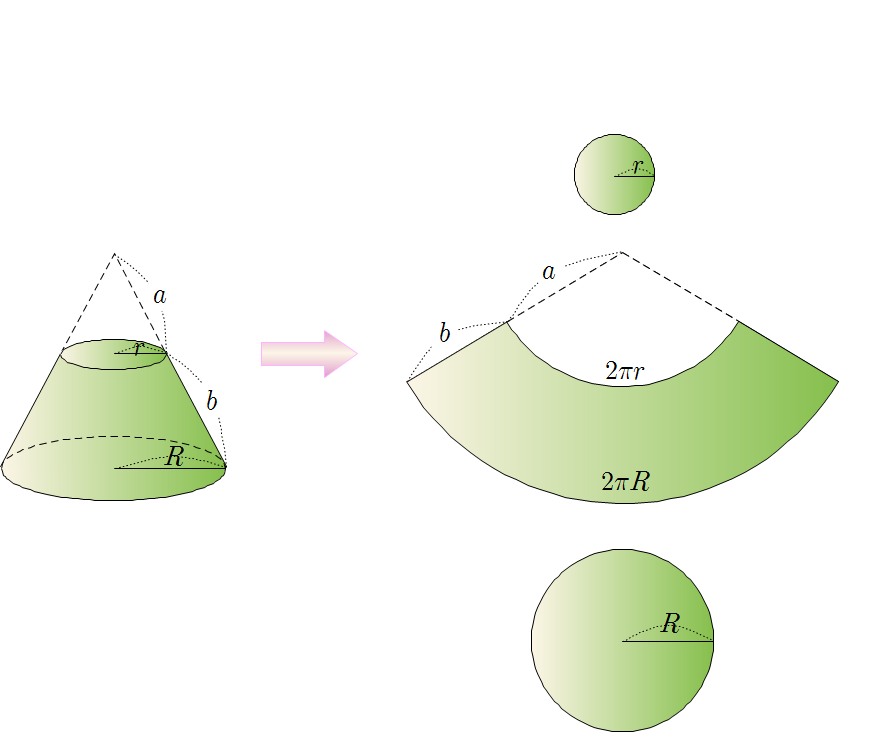
▸ 각뿔대, 원뿔대의 부피 : 원래의 각뿔, 원뿔의 부피에서 잘려 나간 각뿔, 원뿔의 부피를 뺀다.

† 밑면이 정다각형이고 옆면이 모두 합동인 이등변삼각형으로 이루어진 각뿔을 정각뿔이라고 한다.
† 그림과 같이 밑넓이와 높이가 같은 각기둥 모양의 그릇과 각뿔 모양의 그릇으로 실험하여 보면 각뿔의 부피는 각기둥의 부피의 ⅓임을 알 수 있다. 하지만 실험도구를 준비하기 힘들고, 수학적 엄밀성이 떨어지므로 고차원적인 방법을 배우기 전까지는 단순 공식으로 암기한다.

❦ 구의 겉넓이와 부피
❧ 구의 겉넓이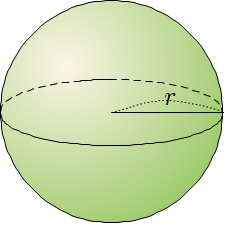
\[(구의 겉넓이)=4\pi r^2\]
❧ 구의 부피
\[(구의 부피)=\frac43\pi r^3\]

† 반지름의 길이가 \(r\)인 구의 겉넓이는 반지름의 길이가 \(r\)인 원의 넓이의 \(4\)배임이 알려져 있다.
† 밑면의 지름의 길이와 높이가 \(2r\)인 원기둥 모양의 그릇에 물을 가득 채운 후, 반지름의 길이가 \(r\)인 구를 그릇에 완전히 잠기도록 넣었다 빼면 원기둥 모양의 그릇에는 처음의 \(\dfrac13\)만큼만의 물이 남아 있음을 알 수 있다. 따라서, \[(구의~부피)=\frac23 \times(원기둥의~부피)=\frac23 \times(\pi r^2 \times 2r)=\frac43 \pi r^3\]
† 밑면의 반지름의 길이가 \(r\), 높이가 \(2r\)인 원뿔, 원기둥과 반지름의 길이가 \(r\)인 구의 부피의 관계
\[(원뿔의~부피)\::\: (구의~부피)\: :\: (원기둥의~부피)\: =\: 1\: :\: 2\: :\: 3\]

Copyright © 2003-2017 trsketch. All Rights Reserved. trsketch.dothome.co.kr
Saturday, July 18, 2015