❦ 다면체
❧ 다면체 : 삼각형, 사각형, 오각형, …의 다각형인 면으로만 둘러싸인 입체도형
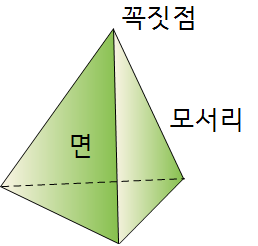
▶ 다면체는 그 면의 개수에 따라 사면체, 오면체, 육면체, …라고 한다.
▶ 각기둥 : 두 밑면이 서로 평행하고 합동인 다각형이며, 옆면이 모두 직사각형인 다면체
▶ 각뿔 : 밑면이 다각형이고 옆면이 모두 삼각형인 다면체
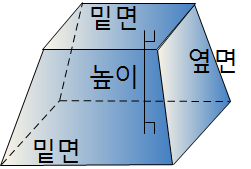
▶ 각뿔대 : 각뿔을 밑면에 평행한 평면으로 잘라서 생기는 두 다면체 중에서 각뿔이 아닌 쪽의 다면체
각뿔대는 밑면의 모양에 따라 삼각뿔대, 사각뿔대, 오각뿔대, …라고 한다.
▶ 정다면체 : 다면체 중에서 각 면이 합동인 정다각형이고, 각 꼭짓점에 모인 면의 개수가 모두 같은 다면체
| 정다면체 | 면의 모양 | 한 꼭짓점에 모인 면의 개수 | 꼭짓점의 개수 | 모서리의 개수 | 면의 개수 |
|
| 정사면체 |
|
정삼각형 | 3 | 4 | 6 | 4 |
| 정육면체 |
|
정사각형 | 3 | 8 | 12 | 6 |
| 정팔면체 |
|
정삼각형 | 4 | 6 | 12 | 8 |
| 정십이면체 |
|
정오각형 | 3 | 20 | 30 | 12 |
| 정이십면체 |
|
정삼각형 | 5 | 12 | 30 | 20 |

† 정다면체가 \(5\)가지 뿐인 이유는 한 꼭짓점에 모이는 정다각형의 내각의 합이 \(360^\circ\)보다 작아야하기 때문이다. 즉, 정삼각형의 한 내각의 크기는 \(60^\circ\)이므로 한 꼭짓점에 \(5\)개까지 모일 수 있고, 정사각형의 한 내각의 크기는 \(90^\circ\)이므로 한 꼭짓점에 \(3\)개까지 모일 수 있다. 정오각형의 한 내각의 크기는 \(108^\circ\)이므로 3개까지 모일 수 있는데, 정육각형은 \(3\)개만 모여도 \(360^\circ\)가 되어 입체도형을 만들 수 없다.
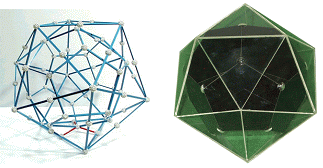
† 각 면이 합동인 정다각형이지만 정다면체가 아닌 예

❦ 회전체
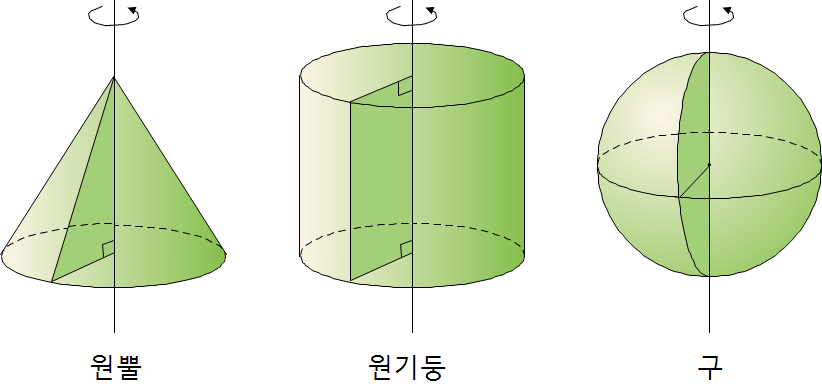
❧ 회전체 : 한 직선을 축으로 하여 평면도형을 1회전 시켜서 생기는 입체도형
▶ 회전축 : 축으로 사용한 직선
▶ 모선 : 회전하면서 옆면을 만드는 선분
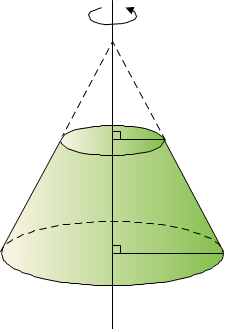
▶ 원뿔대 : 원뿔을 그 밑면에 평행한 평면으로 잘라서 생기는 두 입체도형 중에서 원뿔이 아닌 쪽의 입체도형
|
|
|
❧ 회전체를 평면으로 자른 면
▶ 회전축에 수직인 평면으로 자르면, 그 잘린 면은 항상 원이 된다.
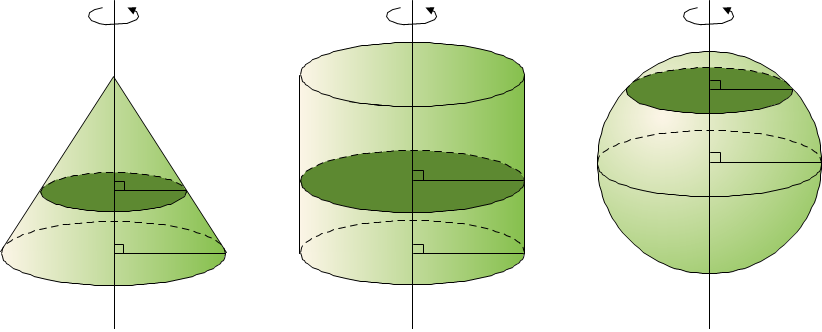
▶ 회전축을 포함하는 평면으로 자르면, 그 잘린 면은 모두 합동이고 회전축을 대칭축으로 하는 선대칭도형이 된다.
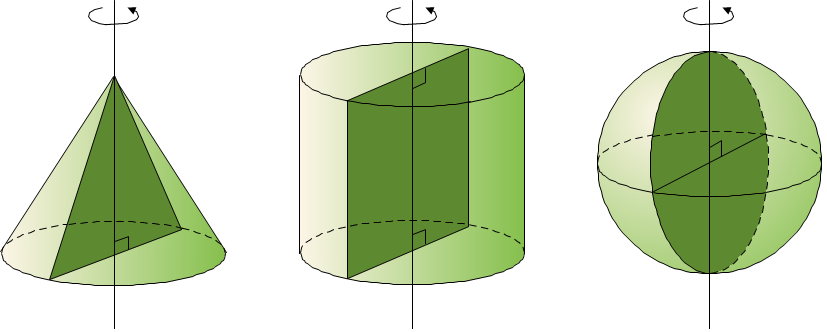
|
♠ How to...
|
☞ 한 걸음 더
♠ 정다면체 이야기
-
플라톤은 우주를 구성하는 네 가지 요소(불, 물, 흙, 공기)를 정다면체에 비유하였다. 가장 가볍고 날카로운 원소인 불은 정사면체, 가장 안정된 원소인 흙은 정육면체, 가장 활동적이고 유동적인 원소인 물은 가장 쉽게 구를 수 있는 정이십면체의 상징으로 간주하였다. 또 정팔면체는 바람에 의해 쉽게 회전하므로 공기의 불안정성을 갖고 있다고 하였다. 마지막으로 정십이면체는 열두 개의 면을 가지고 있고, 또 일주기가 12궁을 가지고 있으므로 우주에 비유하였다.




♠ 원뿔곡선
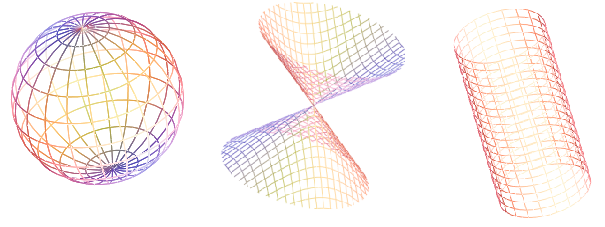
<구, 원뿔, 원기둥을 함수를 이용하여 나타낸 그래프>
♠ 지도 투영법
-
지구는 구체이므로 왜곡없이 세계지도를 표현할 수 없다. 이 문제로 인하여 다양한 지도 투영법이 존재한다.
♠ 회전체(추가)
|
|
Copyright © 2003-2017 trsketch. All Rights Reserved. trsketch.dothome.co.kr
Saturday, July 18, 2015