❦ 원과 부채꼴

❧ 원 \(\rm O\) : 평면 위의 한 점 \(\rm O\)로부터 일정한 거리에 있는 모든 점들로 이루어진 도형

▶ 호 : 원 \(\rm O\) 위의 두 점 \(\rm {A,~B}\)를 잡으면 원은 두 부분으로 나누어지는데 이 두 부분을 각각 호라고 한다. (\(~\rm \overset {\displaystyle\frown}{AB}~\))

▶ 현 : 원 \(\rm O\) 위의 두 점 \(\rm {A,~B}\)를 이은 선분

▶ 할선 : 원 \(\rm O\) 위의 두 점 \(\rm {C,~D}\)를 지나는 직선 \(l\)을 원 \(\rm O\)의 할선이라고 한다.

▶ 부채꼴 : 원 \(\rm O\) 위의 두 반지름 \(\rm OA,~OB\)와 호 \(\rm AB\)로 이루어진 부채 모양의 도형 (부채꼴 \(\rm AOB\))

▶ 중심각 : 두 반지름 \(\rm OA,~OB\)가 이루는 \(\rm \angle AOB\)를 부채꼴 \(\rm AOB\)의 중심각 또는 호 \(\rm AB\)에 대한 중심각이라 하고, 호 \(\rm AB\)를 중심각 \(\rm \angle AOB\)에 대한 호라고 한다.

▶ 활꼴 : 현 \(\rm CD\)와 호 \(\rm CD\)로 이루어진 활 모양의 도형

❧ 부채꼴의 중심각과 호의 길이, 중심각과 넓이 사이의 관계

▶ 한 원에서 중심각의 크기가 같은 두 부채꼴의 호의 길이와 넓이는 각각 같다.

▶ 한 원에서 부채꼴의 호의 길이와 넓이는 각각 중심각의 크기에 정비례한다.

▸ 한 원에서 부채꼴의 현의 길이는 중심각의 크기에 비례하지 않다.

❦ 부채꼴의 호의 길이와 넓이

❧ 원주율 :  원에서 지름의 길이에 대한 원의 둘레의 길이의 비율

☞ 초등학교에서는 원주율로 \(3.14\)를 사용하였으나 원주율은 소수점 뒤에 수가 한없이 계속되는 것으로 알려져 있으므로, 이제부터는 정확한 표현을 위하여 \(\pi\)로 나타내고 '파이'라고 읽는다.

▶ 반지름의 길이가 \(r\)인 원의 둘레의 길이 \(l\)과 넓이 \(S\)는 \[l=2\pi r \qquad S=\pi r^2\]

❧ 부채꼴의 호의 길이와 넓이

▶ 부채꼴의 호의 길이는 중심각의 크기에 비례하므로

\(\eqalign {&360^\circ \::\: (중심각의~크기)\\&=(원의~둘레의~길이)\::\:(부채꼴의~호의~길이)\\ }\)

⇒ \(360^\circ \::\: x^\circ = 2\pi r\::\:l\)

⇒ \(l=\dfrac {x^\circ}{ 360^\circ} \times 2\pi r\)

 

▶ 부채꼴의 넓이는 중심각의 크기에 비례하므로

\(\eqalign {&360^\circ \::\: (중심각의~크기)\\&=(원의~넓이)\::\:(부채꼴의~넓이)\\ }\)

⇒ \(360^\circ \::\: x^\circ = \pi r^2\::\:S\)

⇒ \(S=\dfrac {x^\circ}{ 360^\circ} \times \pi r^2\)

 

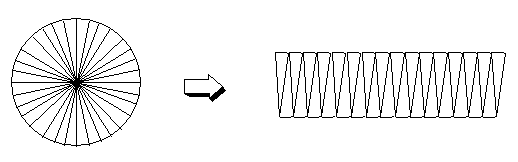
▶ \(S= \dfrac 12 rl\)

부채꼴의 중심각의 크기를 \(x^\circ\), 부채꼴의 호의 길이를 \(l\),

부채꼴의 반지름의 길이를 \(r\), 부채꼴의 넓이를 \(S\)라 하면

\(\begin {align*}S&=\dfrac {x^\circ}{ 360^\circ} \times \pi r^2\\&=\dfrac12 \times r\times\left(2\pi r \times \dfrac {x^\circ}{ 360^\circ}\right)\\&= \dfrac12 rl\end {align*}\)