❦ 다각형의 대각선의 개수

❧ \(n\)각형의 한 꼭짓점에서 그을 수 있는 대각선의 개수는 모두 \((n-3)\)개이다. 이 성질을 이용하여 다각형의 대각선의 개수를 표로 정리하면 다음과 같다.

다각형	다각형의 모양	꼭짓점의 개수	한 꼭짓점에서 그을 수 있는 대각선의 개수	대각선의 개수
사각형		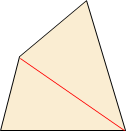\(4\)	\(1\)	\(2\)
오각형		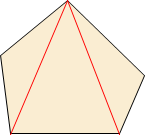\(5\)	\(2\)	\(5\)
육각형		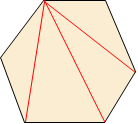\(6\)	\(3\)	\(9\)
칠각형		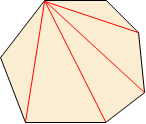\(7\)	\(4\)	\(14\)
\(n\)각형	\(\cdots\)	\(n\)	\(n-3\)	\(\dfrac {n(n-3) } 2\)

 

❦ 삼각형의 내각과 외각

❧ 내각과 외각

▶ 내각 : 다각형에서 이웃하는 두 변으로 이루어진 내부의 각

▶ 외각 : 한 내각의 꼭짓점에서 한 변과 그 변에 이웃한 변의 연장선으로 이루어진 각

 

❧ 삼각형의 내각과 외각

▶ 세 삼각형의 내각의 크기의 합은 \(180^\circ\)이다.

▶ 삼각형의 한 외각의 크기는 그와 이웃하지 않는 두 내각의 크기의 합과 같다.

☞ \(\rm {\overline {AB }} \mathrel {/\!/ } \rm {\overline {CE } }\)이면

\(\angle\rm A=\angle ACE\), \(\angle\rm B=\angle ECD\)이므로

\(\triangle \rm ABC\)의 내각의 크기의 합은

\(\begin {align*} \rm \angle A+\angle B+\angle C&=\rm \angle ACE+\angle ECD+\angle ACB\\&=\rm \angle BCD=180^\circ \end {align*} \)

☞ \(\rm \angle C\)의 외각 \(\rm \angle ACD\)에서

\(\rm \angle ACD=\angle ACE+\angle ECD=\angle A+\angle B\)

 

❦ 다각형의 내각의 크기의 합

❧ 다각형의 한 꼭짓점에서 대각선을 그엇을 때 만들어지는 삼각형의 내각의 총합은 다각형의 내각의 합과 같다.

다각형	다각형의 모양	꼭짓점의 개수	삼각형의 개수	내각의 크기의 합
사각형		\(4\)	\(2\)	\(180^\circ \times2=360^\circ\)
오각형		\(5\)	\(3\)	\(180^\circ \times3=540^\circ\)
육각형		\(6\)	\(4\)	\(180^\circ \times4=720^\circ\)
칠각형		\(7\)	\(5\)	\(180^\circ \times2=900^\circ\)
\(n\)각형	\(\cdots\)	\(n\)	\(n-2\)	\(180^\circ \times(n-2)\)

 

▶ \((정n각형의~한~내각의~크기)=\dfrac { 180^\circ \times(n-2) } {n }\)

 

❦ 다각형의 외각의 크기의 합

❧ \(n\)각형의 외각의 크기의 합은 항상 \(360^\circ\)이다.

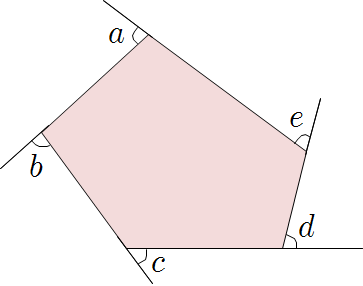
\(\begin {align*}☞~(외각의~크기의~합)&=180^\circ \times n-(내각의~크기의~합)\\&=180^\circ \times n -180^\circ \times(n-2)\\&=180^\circ \times n -180^\circ \times n +180^\circ \times 2\\&=360^\circ\end {align*}\)

▶ \((정n각형의~한~외각의~크기)=\dfrac { 360^\circ} {n }\)

 

♠ How to... 슬라이드 \(n\)을 이용하여 정다각형에 변화를 주도록 한다. 체크박스를 눌러보면서 내각과 외각을 관찰한다. 슬라이드 \(r\)를 이용하여 각의 크기는 변의 길이와 상관이 없음을 확인한다.