❦ 간단한 도형의 작도
❧ 작도 : 눈금 없는 자와 컴퍼스만을 사용하여 도형을 그리는 것
▶ 눈금 없는 자 : 두 점을 연결하는 선분을 그리거나 선분을 연장하는데 사용
▶ 컴퍼스 : 원을 그리거나 주어진 선분의 길이를 옮기는데 사용
❧ 길이가 같은 선분의 작도
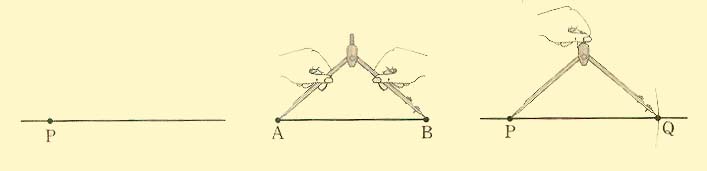
선분 \(\rm {AB }\)에서
(1) 눈금 없는 자를 사용하여 점 \(\rm P\)를 지나는 직선을 그린다.
(2) 컴퍼스로 선분 \(\rm {AB }\)의 길이를 잰다.
(3) 점 \(\rm P\)를 중심으로 하고 선분 \(\rm {AB }\)를 반지름으로 하는 원을 그려 직선과 만나는 점을 \(\rm Q\)라고 하면 선분 \(\rm {AB }\)와 선분 \(\rm {PQ }\)의 길이는 같다.
❧ 크기가 같은 각의 작도
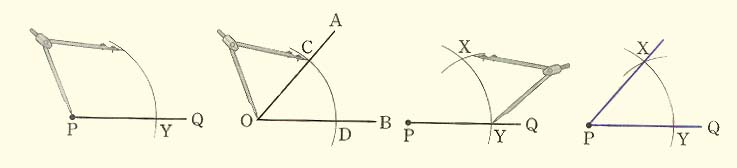
\(\angle \rm {AOB }\)에서
(1) 주어진 반직선 \(\rm {PQ}\)에서 점 \(\rm {P}\)를 중심으로 적당한 원을 그려 반직선 \(\rm {PQ}\)와 만나는 점을 \(\rm {Y}\)라 한다.
(2) 점 \(\rm {O}\)를 중심으로 선분 \(\rm {PY}\)를 반지름으로 하는 원을 그려 반직선 \(\rm {OA}\), \(\rm {OB}\)와 만나는 점을 각각 \(\rm {C}\), \(\rm {D}\)라 한다.
(3) 점 \(\rm {Y}\)를 중심으로 선분 \(\rm {CD}\)를 반지름으로 하는 원을 그려 최초 그린 원과 만나는 점을 \(\rm {X}\)라 한다.
(4) 반직선 \(\rm {PX}\)를 그리면 \(\angle \rm {XPY }\)가 \(\angle \rm {AOB }\)와 크기가 같다.
† 작도에서 길이를 재는 도구는 컴퍼스임에 주의한다.
❦ 삼각형의 작도
❧
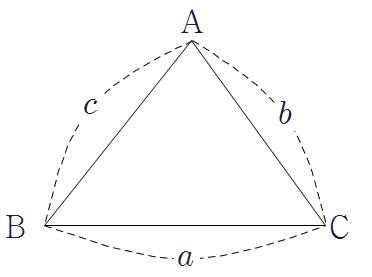삼각형 \(\rm {ABC}\) (\(\triangle \rm {ABC}\))
▶ 세 꼭짓점이 \(\rm A\), \(\rm B\), \(\rm C\)인 삼각형을 삼각형 \(\rm ABC\)라 하고, 이것을 기호로 \(\triangle \rm {ABC}\)와 같이 나타낸다.
이때 변 \(\rm BC\)와 마주 보는 \(\angle \rm {A }\)를 변 \(\rm BC\)의 대각이라 하고, \(\angle \rm {A }\)와 마주 보는 변 \(\rm BC\)를 \(\angle \rm {A }\)의 대변이라고 한다.
❧ 삼각형의 작도
▶ 세 변의 길이(\(a,~b,~c\))가 주어졌을 때
(1) 직선 \(l\)을 긋고, 그 위에 선분 \(a\)와 길이가 같은 선분 \(\rm BC\)를 그린다.
(2) 점 \(\rm B\)를 중심으로 하고 선분 \(a\)를 반지름으로 하는 원을 그린다.
(3) 점 \(\rm C\)를 중심으로 하고 선분 \(b\)를 반지름으로 하는 원을 그려, (2)의 원과 만나는 점을 \(\rm A\)라고 한다.
(4) 점 \(\rm A\)와 \(\rm B\), 점 \(\rm A\)와 \(\rm C\)를 각각 이어서 만든 \(\triangle \rm {ABC}\)가 작도하고자 하는 삼각형이다.
▶ 두 변의 길이(\(b,~c\))와 그 끼인 각(\(\angle \rm {A}\))이 주어졌을 때
(1) \(\angle \rm {A}\)와 크기가 같은 \(\angle \rm {XAY}\)를 작도한다.
(2) 점 \(\rm A\)를 중심으로 하고, 선분 \(c\)를 반지름으로 하는 원을 그려 반직선 \(\rm {AY}\)와 만나는 점을 \(\rm B\)라고 한다.
(3) 점 \(\rm A\)를 중심으로 하고, 선분 \(b\)를 반지름으로 하는 원을 그려 반직선 \(\rm {AX}\)와 만나는 점을 \(\rm C\)라고 한다.
(4) 두 점 \(\rm B\), \(\rm C\)를 이어서 만든 \(\triangle \rm {ABC}\)가 작도하고자 하는 삼각형이다.
▶ 한 변의 길이(\(a\))와 양 끝각(\(\angle \rm {B}\), \(\angle \rm {C}\))이 주어졌을 때
(1) 직선 \(l\)을 긋고, 그 위에 선분 \(a\)와 길이가 같은 선분 \(\rm {BC}\)를 그린다.
(2) \(\angle \rm {B}\)와 크기가 같은 \(\angle \rm {XBC}\)를 작도한다.
(3) \(\angle \rm {C}\)와 크기가 같은 \(\angle \rm {YCB}\)를 작도한다.
(4) 두 반직선 \(\rm {BX}\)와 \(\rm {CY}\)가 만나는 점을 \(\rm A\)라고 하면 \(\triangle \rm {ABC}\)가 작도하고자 하는 삼각형이다.
|
♠ How to...
|
† 삼각형에서 세 변과 세 각을 삼각형의 6요소라고 한다.
† \(\triangle\rm {ABC}\)에서 \(\angle\rm {A}\), \(\angle\rm {B}\), \(\angle\rm {C}\)의 대변 \(\rm {BC}\), \(\rm {CA}\), \(\rm {AB}\)를 각각 \(a\), \(b\), \(c\)로 나타내기도 한다.
† 두 변과 끼이지 않은 한 내각이 주어질 때 삼각형을 유일하게 작도할 수 없는 경우가 존재한다.
❦ 삼각형의 합동조건
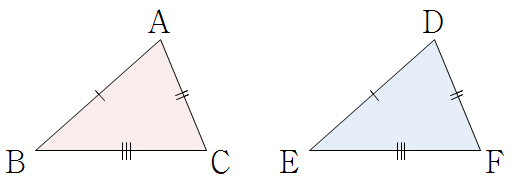
❧ 대응 : 서로 합동인 두 도형을 완전히 포개었을 때, 포개어지는 꼭짓점과 꼭짓점, 변과 변, 각과 각은 각각 대응한다고 한다.
❧ 합동 : 모양과 크기가 같아서 포개었을 때 완전히 겹쳐지는 두 도형
▶ 합동인 도형의 성질
- 대응하는 변의 길이는 각각 같다.
- 대응하는 각의 크기는 각각 같다.
▶ \(\triangle \rm {ABC}\)와 \(\triangle \rm {DEF}\)의 합동
\[\triangle \rm {ABC}\equiv\triangle \rm {DEF}\]
❧ 삼각형의 합동조건
두 삼각형은 다음의 각 경우에 서로 합동이다.
▶ 대응하는 세 변의 길이가 각각 같을 때(SSS 합동)
▶ 대응하는 두 변의 길이가 각각 같고, 그 끼인 각의 크기가 같을 때(SAS 합동)
▶ 대응하는 한 변의 길이가 같고, 그 양끝각의 크기가 각각 같을 때(ASA 합동)
 |
\(\rm {\overline {AB }=\overline {DE }\\ \overline {AC }=\overline {DF }\\ \overline {BC }=\overline {EF }}\) 이면 \(\triangle \rm {ABC}\equiv\triangle\rm {DEF}\) |
 |
\(\eqalign {\rm {\overline {AB }=\overline {DE }\\ \overline {BC }=\overline {EF }\\ \angle ABC = \angle DEF}}\) 이면 \(\triangle \rm {ABC}\equiv\triangle\rm {DEF}\) |
 |
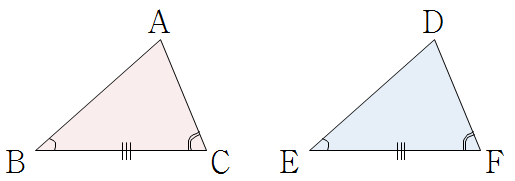\(\eqalign {\rm {\overline {BC }=\overline {EF }\\ \angle ABC = \angle DEF\\ \angle ACB = \angle DFE}}\) 이면 \(\triangle \rm {ABC}\equiv\triangle\rm {DEF}\) |
† \(\triangle \rm {ABC}\equiv\triangle \rm {DEF}\) : 합동이다.
\(\triangle \rm {ABC}=\triangle \rm {DEF}\) : 넓이가 같다.
† 합동을 나타낼 때는 대응하는 꼭짓점의 순서를 지키도록 한다.
☞ 한 걸음 더
-
주어진 정육면체의 부피의 두배의 부피를 갖는 정육면체의 모서리를 작도하는 문제
-
임의의 각을 삼등분하는 문제
-
주어진 원과 동일한 면적을 갖는 정사각형을 작도하는 문제
Copyright © 2003-2017 trsketch. All Rights Reserved. trsketch.dothome.co.kr
Saturday, July 18, 2015