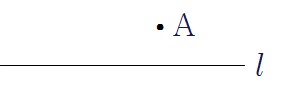❦ 점, 선, 면의 성질

❧ 도형의 기본 요소 : 점, 선, 면

❧ 교점 : 선과 선 또는 선과 면이 만나서 생기는 점

❧ 교선 : 면과 면이 만나서 생기는 선

❧ 선의 종류

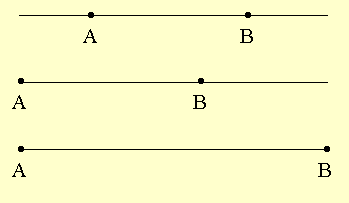
▶ 직선 \(\rm AB\) : \(\rm \overleftrightarrow {AB}\)

▶ 반직선 \(\rm AB\) : \(\rm \overrightarrow {AB}\)

▶ 선분 \(\rm AB\) : \(\rm \overline {AB}\)

 

❧ 두 점 \(\rm A,~B\) 사이의 거리 : 두 점 \(\rm A,~B\)를 이을 수 있는 선 중에서 길이가 가장 짧은 것은 선분 \(\rm AB\)이다. 이때 선분 \(\rm AB\)의 길이를 두 점 \(\rm A,~B\) 사이의 거리라 한다.

▶ 두 선분 \(\rm AB\)와 \(\rm CD\)의 길이가 같다. : \(\rm \overline {AB}=\overline {CD}\)

 

❧ 중점 : 선분 \(\rm AB\) 위의 점 \(\rm M\)에 대하여 \(\rm \overline {AM}=\overline {BM}\)일 때, 점 \(\rm M\)을 선분 \(\rm AB\)의 중점이라고 한다.

 

 

❦ 각

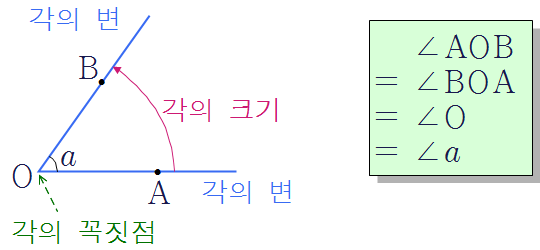
❧ 각 \(\rm AOB\) : 점 \(\rm O\)에서 시작하는 두 반직선 \(\rm OA,~OB\)로 이루어진 도형을 각 \(\rm AOB\)라 하고, 이것을 기호로 \[\rm \angle AOB\]와 같이 나타낸다.

 

❧ 크기에 따른 각의 종류

▶ 예각 : \(0^\circ\)보다 크고 \(90^\circ\)보다 작은 각

▶ 직각 : \(90^\circ\)

▶ 둔각 : \(90^\circ\)보다 크고 \(180^\circ\)보다 작은 각

▶ 평각 : \(180^\circ\)

♠ How to... 점 \(\rm B\)를 끌어 변화를 관찰한다.

 

 

❧ 각의 성질

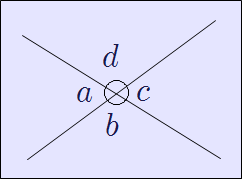
▶ 교각 : 서로 다른 직선이 한 점에서 만날 때 생기는 사잇각

▶ 맞꼭지각 : 교각에서 서로 마주보는 각

▶ 맞꼭지각의 크기는 서로 같다.

\(\left. \begin{align}\angle a+\angle b&=180^\circ\\\angle b+\angle c&=180^\circ\\\end{align} \right\}\quad\Rightarrow  \angle a=\angle c\) 같은 방법으로 \(\angle b=\angle d\)

▶ 두 선분 \(\rm {AB}\)와 \(\rm {CD}\)의 교각이 직각일 때, 두 선분은 서로 직교한다고 한다.

\[\rm \overline{AB}\bot \overline{CD}\]

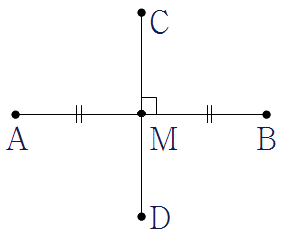이때 두 선분 \(\rm {AB}\)와 \(\rm {CD}\)는 서로 수직이고, 한 선분은 다른 선분의 수선이다.

▶ 선분 \(\rm {AB}\)의 중점 \(\rm M\)을 지나고 선분 \(\rm {AB}\)에 수직인 선분 \(\rm {CD}\)를 선분 \(\rm {AB}\)의 수직이등분선이라고 한다.

 

▶ 그림과 같이 직선 \(l\) 위에 있지 않은 점 \(\rm P\)에서 직선 \(l\)에 수선을 그어서 생기는 교점을 \(\rm H\)라고 할 때, 점 \(\rm H\)를 점 \(\rm P\)에서 직선 \(l\)에 내린 수선의 발이라고 한다.

 

❦ 위치 관계

❧ 점과 직선의 위치 관계

점 \(\rm A\)는 직선 \(l\) 위에 있다.	점 \(\rm A\)는 직선 \(l\) 위에 있지 않다.

 

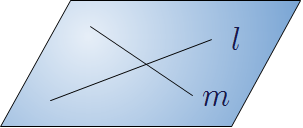
❧ 한 평면 위에서 두 직선의 위치 관계

한 점에서 만난다.	평행하다.\((l\mathrel {/\! /}m)\)	일치한다.

 

❧ 공간에서 서로 다른 두 직선의 위치 관계

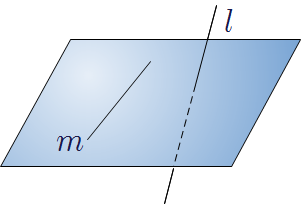한 점에서 만난다.	평행하다.\((l\mathrel {/\! /}m)\)	꼬인 위치에 있다.
한 평면 위에 있다.		한 평면 위에 있지 않다.

 

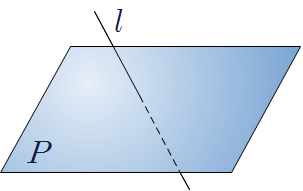
❧ 공간에서 직선과 평면의 위치 관계

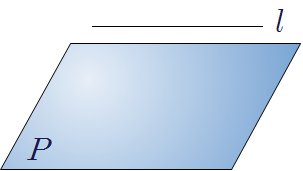직선이 평면에 포함된다.	한 점에서 만난다.	평행하다.\((l\mathrel {/\! /} P)\)

 

❧ 공간에서 두 평면의 위치 관계

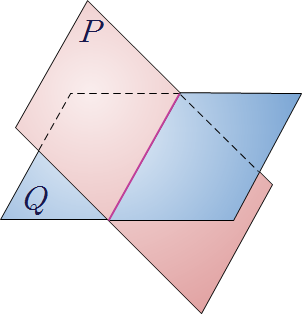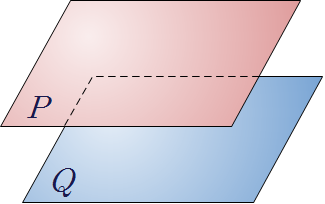한 직선에서 만난다.	평행하다.\((P\mathrel {/\! /} Q)\)	일치한다.

 

❧ 공간에서 직선과 평면이 직교

오른쪽 그림과 같이 직선 \(l\)이 평면 \(P\)와 한 점에서 만나고 교점을 지나는 평면 위의 모든 직선과 서로 수직일 때, 직선 \(l\)과 평면 \(P\)는 서로 수직이다 또는 서로 직교한다고 하고, 이것을 기호로 \[l\mathrel{\bot} P\]와 같이 나타낸다.
이 때 직선 \(l\)을 평면 \(P\)의 수선이라고 한다.

 

❦ 평행선의 성질

❧ 동위각과 엇각

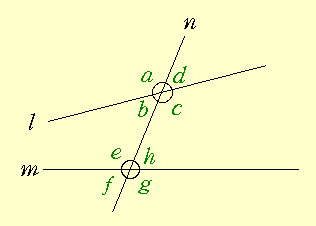오른쪽 그림과 같이 두 직선 \(l,~m\)이 다른 한 직선 \(n\)과 만날 때 생기는 \(8\)개의 각 중에서
\(\angle a\)와 \(\angle e\), \(\angle b\)와 \(\angle f\), \(\angle c\)와 \(\angle g\), \(\angle d\)와 \(\angle h\)
를 각각 서로 동위각이라고 한다. 또,
\(\angle b\)와 \(\angle h\), \(\angle c\)와 \(\angle e\)
를 각각 서로 엇각이라고 한다.

 

❧ 평행선과 동위각

서로 다른 두 직선이 한 직선과 만날 때

(1) 두 직선이 서로 평행하면 동위각의 크기는 서로 같다.

(2) 동위각의 크기가 서로 같으면 그 두 직선은 서로 평행하다.

 

❧ 평행선과 엇각

서로 다른 두 직선이 한 직선과 만날 때

(1) 두 직선이 서로 평행하면 엇각의 크기는 서로 같다.

(2) 엇각의 크기가 서로 같으면 그 두 직선은 서로 평행하다.