❦ 줄기와 잎 그림
❧ 줄기와 잎 그림 : 자료의 값을 큰 자리의 수와 작은 자리의 수로 구분하여 세로줄의 왼쪽에는 큰 자리의 수를, 세로줄의 오른쪽에는 큰 자리의 수에 해당하는 작은 자리의 수를 기록하여 나타낸 그림
▶ 줄기와 잎 그림의 예
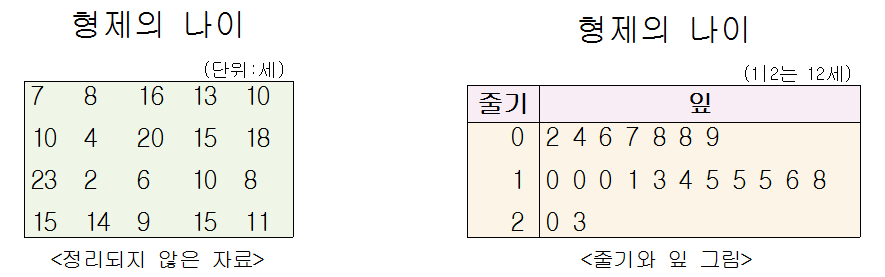
|
♠ How to...
|
❦ 도수분포표
❧ 용어 정리
▶ 변량 : 자료를 수량으로 나타낸 것
▶ 계급 : 변량을 일정한 간격으로 나눈 구간
▶ 계급의 크기 : 구간의 너비
▶ 계급값 : 계급을 대표하는 값으로서 계급의 가운데 값\[(계급값)=\frac{ (계급의~양~끝값의~합)}{ 2}\]
▶ 도수 : 각 계급에 속하는 자료의 수
▶ 도수분포표 : 주어진 자료를 몇 개의 계급으로 나누고, 각 계급에 속하는 도수를 조사하여 나타낸 표
▶ 도수분포표의 예


† 일반적으로 도수분포표를 만들 때, 자료의 분포 상태를 잘 나타내기 위해서 계급의 크기는 모두 같게 하고 계급의 개수는 자료의 양에 따라 보통 \(5\)~\(15\)개 정도로 하는 것이 좋다.
❦ 도수분포표에서의 평균
❧ \((도수분포표에서의~평균)=\dfrac{ \{ (계급값)\times(도수)\}의~총합}{ (도수)의~총합 }\)
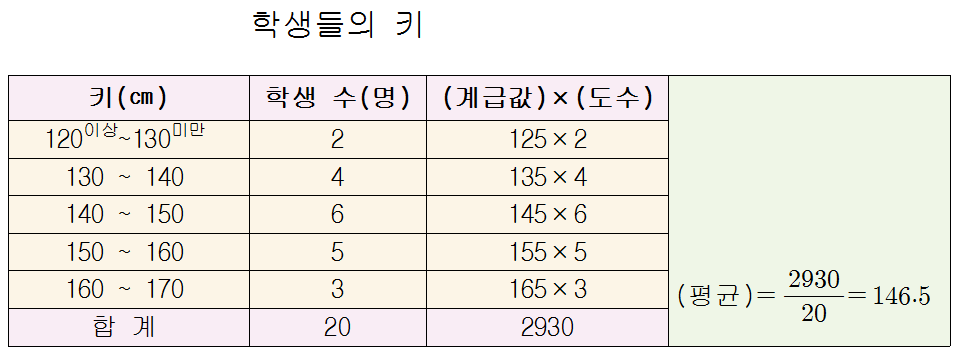

† 도수분포표에서는 원래의 자료를 알 수는 없으므로 정확한 평균을 구할 수는 없다. 도수분포표에서 평균을 구할 때 계급값을 이용하는 것은 바로 이러한 이유 때문이다.
❦ 히스토그램과 도수분포다각형
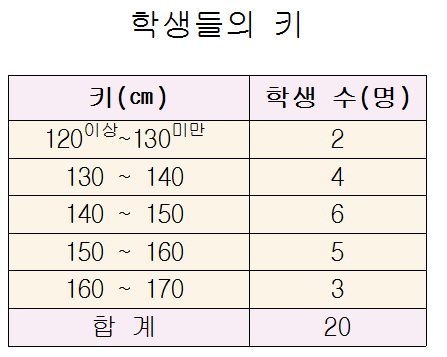
❧ 히스토그램
(1) 가로축에는 각 계급의 양 끝값을 써넣는다.
(2) 세로축에는 도수를 써넣는다.
(3) 각 계급의 크기를 가로로, 도수를 세로로 하는 직사각형을 차례로 그린다.
 |
|
❧ 도수분포다각형
(1) 히스토그램의 각 직사각형의 윗변의 중앙에 점을 찍는다.
(2) 히스토그램의 양 끝에 도수가 \(0\)인 계급이 있는 것으로 생각하여 그 중앙에 점을 찍는다.
(3) 위에서 찍은 점을 선분으로 연결한다.
 |
|
♠ How to...
- 입력한 자료를 모두 선택한다.
- 툴바에서 [일변량 분석]을 클릭한다.
- 새로 열린 창에서 슬라이드를 이용하여 계급의 개수를 조절한다.
- 슬라이드가 있는 줄의 우측에 있는 사각형 버튼을 클릭하여 [선택사항]을 설정한다. 여기에서는 [보이기]에서 히스토그램/도수분포표/도수분포다각형을 모두 체크한다.
- [선택사항]버튼의 우측에 있는 버튼을 클릭하여 [기하창에 복사]를 실행하고 팝업 창을 닫는다.

† 히스토그램의 각 직사각형에서 가로의 길이인 계급의 크기는 일정하므로 직사각형의 넓이는 세로의 길이인 각 계급의 도수에 정비례한다.
† 히스토그램과 막대그래프의 차이
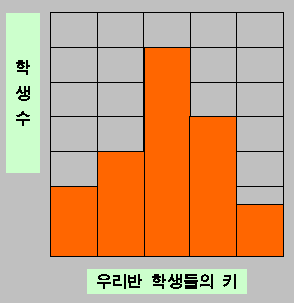

[히스토그램] [막대그래프]
* 막대그래프로 나타내는 예 : 좋아하는 연예인, 좋아하는 색상 등 비연속적인 자료
* 히스토그램으로 나타내는 예 : 몸무게, 키, 성적, 온도 등 연속적인 자료
† 히스토그램의 직사각형의 넓이의 합과 도수분포다각형과 가로축으로 둘러싸인 부분의 넓이는 같다.
❦ 상대도수
❧ 상대도수
\((어떤~계급의~상대도수)=\dfrac{ (그~계급의~도수)}{ (도수의~총합)}\)
❧ 상대도수의 분포표 : 도수분포표에서 계급의 도수 대신 상대도수를 나타낸 표
▶ 상대도수를 이용하면 각 계급의 도수가 전체에서 차지하는 비율을 한 눈에 알 수 있다.
▶ 상대도수는 \(0\) 이상 \(1\) 이하의 수로 나타내어지며, 상대도수의 합은 항상 \(1\)이다.
❧ 상대도수의 그래프 : 도수분포표를 히스토그램이나 도수분포다각형으로 나타내는 방법과 같다.


† 상대도수의 분포표를 만들다보면 상대도수의 총합이 \(1\)이 아닌 경우가 있다. 이것은 상대도수를 소수로 표현하면서 소수점 아래의 반올림 때문에 발생하는 현상이다. 만일 상대도수를 분수로 나타낸다면 이러한 일은 생기지 않겠지만 소수로 표현해야하기 때문에 반올림을 할 때 필요에 따라서는 인위적인 조작이 필요할 수도 있다.
☞ 한 걸음 더
♠
윈도우 계산기를 이용한 평균 구하기
- [보기>통계용] 선택
- [자료 입력-Add클릭]의 과정을 반복하여 모든 자료를 입력한다.
- [\(\bar x\)]버튼을 눌러 평균을 구한다.
- [CAD]버튼은 입력한 모든 자료를 삭제하는 것이고, [C]버튼은 창에 출력되어있는 값을 삭제하는 것이다.
♠ 스프레드시트를 이용하여 평균 구하기
- A열에 자료를 순서대로 입력한다.
- 비어있는 적절한 셀을 선택하고, 함수 마법사를 실행한다.
- 함수 중 AVERAGE를 선택한다.
- 범위는 A열에 자료가 있는 부분으로 한다.
- 범위를 적절히 선택하였으면 [확인]버튼을 누른다.
♠ 통계관련 추천 사이트
- 통계청(http://kostat.go.kr/portal/korea/index.action)
- 어린이 통계 동산(http://kostat.go.kr/community/nkids/index.action)
Copyright © 2003-2017 trsketch. All Rights Reserved. trsketch.dothome.co.kr
Saturday, July 18, 2015