❦ 함수의 뜻과 표현

❧ 변수 : 식에서 \(x,~y\)와 같이 여러 가지로 변하는 값을 나타내는 문자

예) \(500\)원짜리 지우개 \(x\)개의 금액은 \(y\)원이다.

⇒ \(y=500x\) : 변수는 \(x,~y\)

 

❧ 함수 : 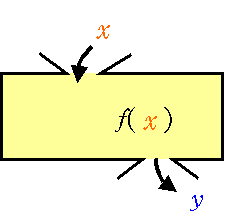두 변수 \(x,~y\)에 대하여 \(x\)의 값이 변함에 따라 \(y\)의 값이 하나씩 정해질 때, \(y\)를 \(x\)의 함수라 하고, 이것을 기호로 \[y=f(x)\]와 같이 나타낸다.

예) \(y=500x\)에서 \(y\)는 \(x\)의 함수이고, \(f(x)=500x\)로 나타내기도 한다.

 

❧ 함숫값 : 함수 \(y=f(x)\)에서 \(x\)의 값에 따라 하나로 정해지는 \(y\)의 값을 \(x\)의 함숫값이라고 하며, 이것을 기호로 \[f(x)\]와 같이 나타낸다.

예) \(y=500x\)에서 \(x=2\)일 때, \(y=1000\)이다. 이때 \(1000\)은 \(x=2\)에서의 \(y=500x\)의 함숫값이다.\[f(2)=1000\]

 

 

❦ 순서쌍과 좌표

❧ 좌표 : 수직선 위의 점에 대응하는 수

수 \(a\)가 점 \(\rm P\)의 좌표일 때, 이것을 기호로 \[\rm P(\it a)\]와 같이 나타낸다.

 

❧ 순서쌍 : 두 수의 순서를 생각하여 짝지어 나타낸 쌍

\[(x,~y)\]

 

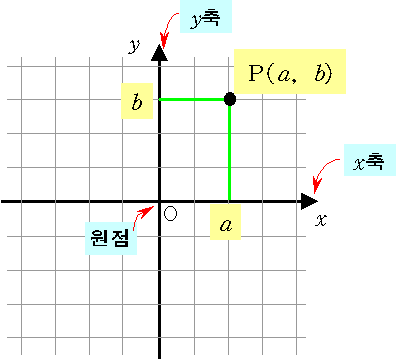
❧ 좌표축 : 그림과 같이 두 수직선을 점 \(\rm O\)에서 서로 수직으로 만나도록 그릴 때, 가로의 수직선을 \( x\)축, 세로의 수직선을 \(y\)축이라 하고, \(x\)축, \(y\)축을 통틀어 좌표축이라고 한다.

 

❧ 원점 : 두 좌표축의 교점 \(\rm O\)

 

❧ 좌표평면 : 좌표축이 정해져 있는 평면

 

❧ 사분면 : 좌표평면을 네 부분으로 나눌 때, 이들을 각각

제1사분면, 제2사분면, 제3사분면, 제4사분면

이라고 한다.