❦ 등식과 방정식

❧ 등식 : 등호 '\(=\)'를 사용하여 두 수 또는 두 식이 같음을 나타낸 식

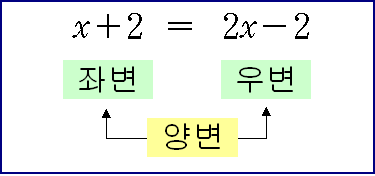▶ 등식에서 등호의 왼쪽 부분을 좌변, 오른쪽 부분을 우변이라고 하며, 좌변과 우변을 통틀어 양변이라고 한다.

 

❧ 방정식 : 미지수 \(x\)의 값에 따라 참이 되기도 하고 거짓이 되기도 하는 등식을 \(x\)에 관한 방정식이라고 한다.

▶ 미지수 : 방정식에 있는 \(x\)등의 문자

▶ 방정식의 해(근) : 방정식을 참이 되게 하는 미지수 \(x\)의 값

▶ 방정식을 푼다 : 방정식의 해(근)을 구하는 것

  예) 방정식 \(x+1=3\)의 해는 \(x=2\)이다.

 

❧ 항등식 : 미지수 \(x\)에 어떤 값을 대입하여도 항상 참이 되는 등식을 \(x\)에 관한 항등식이라고 한다.

  예) \(x+2x=3x,~4x-3x=x\)

 

❦ 등식의 성질

❧ 등식의 양변에 같은 수를 더하여도 등식은 성립한다.

\[a=b이면 ~ a+c=b+c\] 

❧ 등식의 양변에 같은 수를 빼어도 등식은 성립한다.

\[a=b이면 ~ a-c=b-c\] 

❧ 등식의 양변에 같은 수를 곱하여도 등식은 성립한다.

\[a=b이면 ~ a \times c=b \times c\] 

❧ 등식의 양변에 \(0\)이 아닌 같은 수로 나누어도 등식은 성립한다.

\[a=b이면 ~ \frac{a}{c}=\frac{b}{c}~(단,~c\ne0)\]

  

❦ 일차방정식

❧ 이항 : 등식의 성질을 이용하여 등식의 어느 한 변에 있는 항을 부호를 바꾸어 다른 변으로 옮기는 것

\(\eqalign{x+1&=2\\x+1-1&=2-1\\x&=2-1\\x&=1}\)

\(\eqalign{x+1&=2\\x&=2-1\\x&=1}\)

❧ 일차방정식 : 방정식의 우변에 있는 모든 항을 좌변으로 이항하여 정리하였을 때

(일차식)=0

의 꼴로 나타내어지는 방정식을 일차방정식이라고 한다.

 

 

❧ 일차방정식의 풀이

(1) 계수가 소수나 분수가 있으면 양변에 적당한 수를 곱하여 계수를 정수로 고친다.

(2) 괄호가 있으면 괄호를 푼다.

(3) 미지수 \(x\)를 포함한 항은 좌변으로, 상수항은 우변으로 이항한다.

(4) 양변을 정리하여 \(ax=b(a\ne0)\)의 꼴로 고친다.

(5) \(x\)의 계수 \(a\)로 양변을 나눈다.

예1) \(\begin{align}2x+2&=-x+8\\2x+x&=8-2\\3x&=6\\x&=2\end{align}\)	예2) \(\begin{align}3(x-1)&=x+1\\3x-3&=x+1\\3x-x&=1+3\\2x&=4\\x&=2\end{align}\)
예3) \(\begin{align}\frac12 x +3&=\frac13 x +1\\6\times \left( \frac12 x +3 \right)&=6\times \left(\frac13 x +1\right)\\3x+18&=2x+6\\x&=-12\end{align}\)
예4) \(\begin{align}0.2x+1&=0.4x-2\\10\times(0.2x+1)&=10\times(0.4x-2)\\2x+10&=4x-20\\-2x&=-30\\x&=15\end{align}\)

       

❦ 일차방정식의 활용

❧ 일차방정식을 활용하여 문제를 해결하는 순서

(1) 문제의 뜻을 파악하고, 무엇을 미지수로 놓을지 결정한다.

(2) 등식 관계가 있는 수량을 찾아 일차방정식으로 나타낸다.

(3) 일차방정식을 푼다.

(4) 구한 해가 문제의 뜻에 맞는지 확인한다.

  예) 형제의 나이의 합이 \(50\)살이다. 형이 동생보다 \(12\)살 많다고 할 때, 동생의 나이를 구하여라.

(1) 동생의 나이를 \(x\)살이라고 한다.

(2) 형의 나이는 \(x+12\)살이므로
     \(x+x+12=50\)

(3) \(2x+12=50\)에서 \(x=19\)

(4) \(19+19+12=50\)이므로, 동생의 나이는 \(19\)살이다.