❦ 문자를 사용한 식
❧ 문자를 사용하면 수량 사이의 관계를 간단히 나타낼 수 있다.
▶ \(1\)개에 100원하는 사탕 \(x\)개의 가격
\(\eqalign { (사탕의~ 가격)&=(사탕~ 1개의~ 가격)\times(사탕의~ 개수)\\ &=100\times x(원) }\)
❧ 곱셈 기호의 생략
▶ 수와 문자의 곱에서 곱셈 기호 \(\times\)는 생략한다.
(1) 수는 문자 앞에 쓴다.
예) \(2\times x=2x,~a \times 3=3a\)
(2) 수가 \(1\) 또는 \(-1\)인 경우 \(1\)은 생략한다.
예) \(1\times x=x,~a \times (-1)=-a\)
▶ 문자와 문자의 곱에서 곱셈 기호 \(\times\)는 생략한다.
(1) 문자는 보통 알파벳 순서로 쓴다.
예) \(b\times a \times2 =2ab\)
(2) 같은 문자의 곱은 거듭제곱의 꼴로 나타낸다.
예) \(a\times a\times b\times5=5a^2 b\)
▶ 괄호가 있는 식과 수의 곱에서 수는 괄호 앞에 쓰고 곱셈 기호 \(\times\)는 생략한다.
예) \((x-2)\times3=3(x-2)\)
❧ 나눗셈 기호의 생략
▶ 문자를 사용한 식에서 나눗셈 기호 \(\div\)는 생략하여 분수의 꼴로 나타낸다.
예) \(a\div b=\dfrac a b \) (단, \( b \ne0)\)

† 다음에 대하여 주의하도록 한다.
☞ \(0.1\times a =0.1a \ne 0.a\)
☞ \(\begin{equation} \left.\begin{aligned} -(a\div2)\\ (-a)\div2=\dfrac{ -a}{ 2}\\ a\div{ (-2)}=\dfrac{ a}{ -2}\end {aligned} \right\} = - \dfrac a2\end{equation}\)
☞ \(x \div yz =\cases{ x \times\dfrac1{ yz} =\dfrac x{ yz}&(○)\\x\div y\times z =x \times \dfrac1y \times z =\dfrac{ xz}y&(×)}\)
[세번째에 대하여는 중2 단항식의 계산에서 자세히 다룬다.]
❦ 식의 값
❧ 대입: 문자를 사용한 식에서 문자 대신 수를 넣는 것
❧ 식의 값: 문자에 수를 대입하여 계산한 값
▶ 예) \(a=2\)일 때, \(-4a\)의 값을 구하여라.
⇒ \(-4a=-4\times a=-4\times2=-8\)

† 문자에 음수를 대입할 때에는 괄호를 사용한다.
- \(a=-2\)일 때, \(3x+1\)의 값은 \(\cases{ 3-2+1 &(×)\\3\times(-2)+1&(○)}\)
- \(x=-3\)일때, \(\cases{ -x^2=-(-3)^2=-9\\(-x)^2=x^2=(-3)^2=9}\)
❦ 단항식과 다항식
❧ 단항식과 다항식
▶
항 : 수 또는 문자의 곱으로만 이루어진 식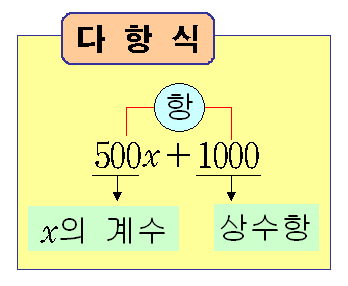
▶ 상수항 : 수로만 이루어진 항
▶ 계수 : 상수항이 아닌 항에서 문자 앞에 곱해진 수
▶ 다항식 : 하나 이상의 항의 합으로 이루어진 식
▶ 단항식 : 하나의 항으로만 이루어진 식
❧ 일차식
▶ 항의 차수 : 항에 포함되어 있는 어떤 문자의 곱해진 개수
예)
\(3x^2\)의 차수는 \(2\)
\(-2b\)의 차수는 \(1\)
▶ 다항식의 차수 : 다항식에서 차수가 가장 큰 항의 차수
예) \(3x^2+4x+5\)의 차수는 \(2\)
▶ 일차식 : 차수가 \(1\)인 다항식
예) \(x+2,~3x-2,~-x+2\)
❦ 일차식의 계산
❧ 단항식과 수의 곱셈 : 수끼리 곱하여 수를 문자 앞에 쓴다.
\(\eqalign{ 5x\times100&=5\times x \times 100\\ &=5 \times100\times x\\&=(5\times100)\times x \\&=500x }\)
❧ 일차식과 수의 곱셈 : 분배법칙을 이용하여 일차식의각 항에 그 수를 곱하여 계산한다.
\(\eqalign{ 2\times(3x+1)&=2\times3x+2\times1 \\&=6x+2 }\)
❧ 일차식과 수의 나눗셈 : 나눗셈을 곱셈으로 고쳐서 계산한다.
\(\bbox[border:1px solid] {\begin{aligned}(2x-4)\div2&=(2x-4)\times\dfrac12\\&=2x\times\dfrac12 -4\times\dfrac12\\&=x-2\end {aligned} }\quad\)
또는 \(\quad\bbox[border:1px solid] { \begin{aligned} (2x-4)\div2&= \dfrac { 2x-4}{ 2}\\&=\dfrac { 2x}{ 2}-\dfrac42\\&=x-2\end {aligned} }\)
❦ 일차식의 덧셈과 뺄셈
❧ 동류항 : 문자와 차수가 같은항
▶ \(3x+2+x+4\)에서 \(3x\)와 \(x\), \(~2\)와 \(4\)는 각각 동류항이다.
▶ \(x^2\)과 \(x^3\)은 문자는 같지만 차수가 다르므로 동류항이 아니다.
▶ \(xy\)와 \(2x\)는 곱해진 문자가 다르므로 동류항이 아니다.

❧ 일차식의 덧셈과 뺄셈
▶ 괄호가 있는 일차식의 덧셈은 분배법칙을 이용하여 괄호를 풀고, 동류항끼리 모아서 계산한다.
▶ 일차식의 뺄셈은 빼는 식의 각 항의 부호를 바꾸어 더한다.
\(\eqalign{ 3(x-2)-2(x+1)&=3x-6-2x-2\\&=3x+(-6)+(-2x)+(-2) \\&=3x+(-2x)+(-6)+(-2) \\&=\{ 3x+(-2x)\}+\{ (-6)+(-2)\}\\&=x-8 }\)
Copyright © 2003-2017 trsketch. All Rights Reserved. trsketch.dothome.co.kr
Saturday, July 18, 2015