❦ 유리수의 덧셈
❧
부호가 같은 두 수의 덧셈
→ 두 수의 절댓값의 합에 공통인 부호를 붙인다.
▶ (양수)\(+\)(양수)
예) \((+2)+(+3)=+(2+3)=+5\)

▶ (음수)\(+\)(음수)
예) \((-2)+(-3)=-(2+3)=-5\)

❧
부호가 다른 두 수의 덧셈
→ 두 수의 절댓값의 차에 절댓값이 큰 수의 부호를 붙인다.
▶ (양수)\(+\)(음수)
예) \((+4)+(-1)=+(4-1)=+3\)
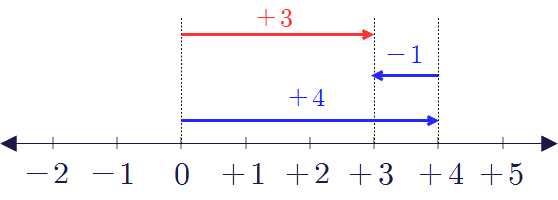
▶ (음수)\(+\)(양수)
예) \((-5)+(+3)=-(5-3)=-2\)


† 절댓값이 같고 부호가 다른 두 수의 합은 \(0\)이다.
❦ 유리수의 덧셈의 계산 법칙
❧ 덧셈의 교환법칙 : 두 수 \(a,~b\)에 대하여
\[a+b=b+a\]
❧ 덧셈의 결합법칙 : 세 수 \(a,~b,~c\)에 대하여
\[(a+b)+c=a+(b+c)\]

† 세 수의 덧셈에서는 \((a+b)+c=a+(b+c)\)이므로 괄호를 사용하지 않고 \(a+b+c\)와 같이 나타낸다.
† 덧셈에서는 결합법칙이 성립하므로 더하는 순서를 바꾸어 계산하면 편리하다.
\(\eqalign {\left(-\frac12\right)+\left(+\frac34\right)+\left(-\frac12\right)&=\left(-\frac12\right)+\left(-\frac12\right)+\left(+\frac34\right)\\&=\biggl\lbrace \left(-\frac12\right)+\left(-\frac12\right)\biggr\rbrace+\left(+\frac34\right)\\&=(-1)+\left(+\frac34\right)=-\frac14} \)
❦ 유리수의 뺄셈
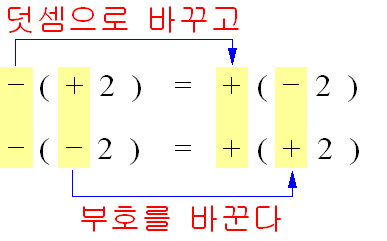
❧ 빼는 수의 부호를 바꾸어 더한다.
예) \((+3)-(+4)=(+3)+(-4)=-1\)
예) \((-3)-(-4)=(-3)+(+4)=+1\)

† 뺄셈에서는 덧셈과 같은 교환법칙과 결합법칙이 성립하지 않는다.
\((-2)-(-3)\neq(-3)-(-2)\)
\(\{ (+1)-(+2) \} -(+3)\neq(+1)- \{ (+2)-(+3) \} \)
❧ 덧셈과 뺄셈의 혼합 계산
(1) 부호가 없는 수는 \(+\)부호를 써 준다.
(2) 뺄셈을 덧셈으로 고친다.
(3) 덧셈에 대한 교환법칙이나 결합법칙을 이용하여 계산한다.
\(\eqalign{ 5-2-(-3)&=(+5)-(+2)-(-3)\\&=(+5)+(-2)+(+3)\\&=\{ (+5)+(-2) \} +(+3)\\&=(+3)+(+3)\\&=+6 }\)
❦ 유리수의 곱셈
❧
부호가 서로 같은 두 수의 곱셈
→ 두 수의 절댓값의 곱에 양의 부호 \(+\)를 붙인다.
▶
(양수)\(\times\)(양수)
예) \((+2)\times(+3)=+(2\times3)=+6\)
▶
(음수)\(\times\)(음수)
예) \((-2)\times(-3)=+(2\times3)=+6\)
❧
부호가 서로 다른 두 수의 곱셈
→ 두 수의 절댓값의 곱에 음의 부호 \(-\)를 붙인다.
▶
(양수)\(\times\)(음수)
예) \((+2)\times(-3)=-(2\times3)=-6\)
▶
(음수)\(\times\)(양수)
예) \((-2)\times(+3)=-(2\times3)=-6\)
❧ (속력)\(\times\)(시간)\(=\)(거리)를 이용하여 다음을 설명할 수 있다.
시속 \(4㎞\)로 동쪽으로 걸어갈 때를 \(+4\)로 나타내면 현재부터
▶ \(2\)시간 후의 위치
 \(\qquad(+4)\times(+2)=+8\)
\(\qquad(+4)\times(+2)=+8\)
▶ \(2\)시간 전의 위치
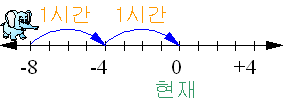 \(\qquad(+4)\times(-2)=-8\)
\(\qquad(+4)\times(-2)=-8\)
시속 \(4㎞\)로 서쪽으로 걸어갈 때를 \(-4\)로 나타내면 현재부터
▶ \(2\)시간 후의 위치
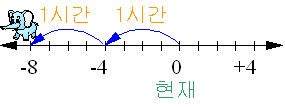 \(\qquad(-4)\times(+2)=-8\)
\(\qquad(-4)\times(+2)=-8\)
▶ \(2\)시간 전의 위치
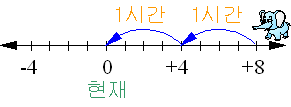 \(\qquad(-4)\times(-2)=+8\)
\(\qquad(-4)\times(-2)=+8\)

† 어떤 수와 \(0\)의 곱은 항상 \(0\)이다.
† \(-2^2\ne(-2)^2 \qquad\implies\qquad\cases { -2^2=-(2\times2)\\\\(-2)^2=(-2)\times(-2) } \)
❦ 유리수의 곱셈의 계산 법칙
❧ 곱셈의 교환법칙 : 두 수 \(a,~b\)에 대하여
\[a\times b=b\times a\]
❧ 곱셈의 결합법칙 : 세 수 \(a,~b,~c\)에 대하여
\[(a\times b)\times c=a\times(b\times c)\]
❧ 분배법칙 : 세 수 \(a,~b,~c\)에 대하여
\[a\times (b+c)=a\times b+a\times c\\(a+b)\times c=a\times c+b\times c\]

† 세 수의 곱셈에서는 \((a\times b)\times c=a\times (b\times c)\)이므로 괄호를 사용하지 않고 \(a\times b\times c\)와 같이 나타낸다.
† 세 개 이상의 수를
곱할 때에는 먼저 곱의 부호를 정하고, 각 수들의 절댓값의 곱에 그 부호를 붙여서 계산하면 편리한 경우가 있다.
이때 곱의 부호는 음수의 개수가 짝수 개이면 '\(+\)', 홀수 개이면 '\(-\)'이다.
❦ 유리수의 나눗셈
❧
부호가 서로 같은 두 수의 나눗셈
→ 두 수의 절댓값의 나눗셈에 양의 부호 \(+\)를 붙인다.
▶
(양수)\(\div\)(양수)
예) \((+12)\div(+4)=+3\quad\Leftarrow\quad(+4)\times(+3)=+12\)
▶
(음수)\(\div\)(음수)
예) \((-12)\div(-4)=+3\quad\Leftarrow\quad(-4)\times(+3)=-12\)
❧
부호가 서로 다른 두 수의 나눗셈
→ 두 수의 절댓값의 나눗셈에 음의 부호 \(-\)를 붙인다.
▶
(양수)\(\div\)(음수)
예) \((+12)\div(-4)=-3\quad\Leftarrow\quad(-4)\times(-3)=+12\)
▶
(음수)\(\div\)(양수)
예) \((-12)\div(+4)=-3\quad\Leftarrow\quad(+4)\times(-3)=-12\)
❧ 역수 : \(4\times\dfrac14=1,~\left(-\dfrac53\right)\times\left(-\dfrac35\right)=1 \)과 같이 어떤 두 수의 곱이 \(1\)이 될 때, 한 수를 다른 수의 역수라고 한다.
\[a의~역수\quad\Rightarrow\quad\frac1a\]
❧
역수를 이용한 나눗셈
→ 나누는 수를 그 역수로 바꾸어 곱셈으로 고쳐서 계산한다.
\[\frac b a\div\frac d c=\frac b a\times\frac c d\]
예) \(\left(-\dfrac56\right)\div\left(+\dfrac23\right)=\left(-\dfrac56\right)\times\left(+\dfrac32\right)=-\dfrac54\)

† \(0\) 을 \(0\)이 아닌 수로 나눈 몫은 항상 \(0\)이다.
† \(0\)은 어떤 수를 곱하여도 \(1\)이 될 수 없으므로 \(0\)의 역수는 생각하지 않는다.
❦ 유리수의 혼합 계산
❧ 덧셈, 뺄셈, 곱셈, 나눗셈이 섞여 있는 식의 경우에는 다음과 같은 순서로 계산할 수 있다.
(1) 거듭제곱이 있으면 거듭제곱을 먼저 계산한다.
(2) 괄호가 있으면 괄호 안을 먼저 계산한다.
(3) 곱셈, 나눗셈을 계산한다.
(4) 덧셈, 뺄셈을 계산한다.
\(\eqalign { \phantom{=}&\bigg[-\dfrac16+\bigg \{ -\dfrac12+\bbox[yellow]{ \bigg(-\dfrac23 \bigg)^2}\div\dfrac43\bigg\}\bigg]\times\bigg(2-\dfrac53\bigg)\\=&\bigg\{ -\dfrac16+\bigg(-\dfrac12+\bbox[pink]{\dfrac49\times\dfrac34}\bigg)\bigg\} \times\bigg(\dfrac63-\dfrac53\bigg)\\=&\bigg\{ -\dfrac16+\bbox[#66ff99]{ \bigg(-\dfrac12+\dfrac13\bigg) }\bigg \} \times\dfrac13 \\=&\bbox[#ccffff]{\bigg\{ -\dfrac16+\bigg(-\dfrac16\bigg)\bigg \} } \times\dfrac13 \\=&\bigg(-\dfrac13\bigg)\times\dfrac13 \\=&-\dfrac19 } \)
☞ 한 걸음 더
♠ 사칙 연산 기호의 유래
- 사칙 연산의 기호는 오랜 세월에 걸쳐 변화하면서 지금의 모양이 되었다. 정확한 기원은 알 수 없으나 대체로 다음과 같은 이야기가 설득력이 있다.
\(-\)기호 : \(1489\)년 독일의 비트만이 발행한 산수책에 처음으로 등장한다. '모자란다'라는 라틴어 단어 minus의 약자 \(\overline m\)를 빠르게 쓰다 \(-\) 모양으로 바뀐것으로 보인다.
\(\times\)기호 : \(1631\)년 영국의 오트레드가 '수학의 열쇠'라는 책에서 처음으로 사용한 것으로 알려져 있다.
\(\div\)기호 : \(\div\)는 분수의 꼴을 추상화한 것으로 오래전부터 사용되어 왔다고 알려져 있다. 비를 나타내는 기호 \(:\)에서 유래된 것이라는 가설도 있다.
♠ 계산기의 사용
- MS Windows의 보조프로그램 계산기의 간단한 활용
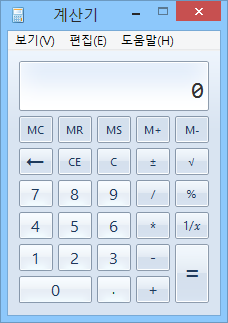

- Backspace : 입력한 숫자를 한 자리씩 지운다.
- CE : 현재 창에 나타난 숫자를 지운다.
- C : 계산 결과를 모두 지운다.
- MC : 기억시켜둔 수를 지운다.
- MR : 기억시켜둔 수를 불러온다.
- MS : 현재 계산 결과를 기억시킨다.
- M+ : 기억시켜둔 수에 현재의 결과를 더한다.
- M- : 기억시켜둔 수에 현재의 결과를 뺀다.
- +/- : 숫자의 부호를 바꾼다.
- +, -, *, / : 순서대로 덧셈, 뺄셈, 곱셈, 나눗셈
- % : 곱셈결과를 백분율로 나타낸다.
- 1/x : 역수를 구한다.
Copyright © 2003-2017 trsketch. All Rights Reserved. trsketch.dothome.co.kr
Saturday, July 18, 2015