❦ 정수와 유리수

❧ 정수 : 양의 정수, \(0\), 음의 정수

▶ 양의 정수 : 자연수에 양의 부호 \(+\)를 붙여 나타낸 수

▶ 음 의 정수 : 자연수에 음의 부호 \(-\)를 붙여 나타낸 수

❧ 유리수 : 분자와 분모가 자연수인 분수에 양의 부호를 붙인 수, 음의 부호를 붙인 수, \(0\)을 통틀어 유리수라고 한다. (단, 분모는 \(0\)이 아니다.)

▶ 모든 자연수는 분수로 나타낼 수 있으므로 모든 정수는 유리수이다.

▶ 정수가 아닌 유리수는 소수로 나타낼 수 있다.

❧ 유리수의 분류

† 앞으로 특별한 언급이 없으면 수라고 하면 유리수를 뜻한다.

† 양수에서 \(+\)부호는 생략하여 나타내기도 한다.

❦ 수직선과 유리수

❧ 수직선: 직선 위에 기준이 되는 점을 \(0\)으로 하여 \(0\)의 오른쪽으로 양수를, 왼쪽으로 음수를 대응시킨 직선

❧ 절댓값: 수직선 위에서 어떤 수를 나타내는 점과 원점 사이의 거리를 그 수의 절댓값이라 하고, 기호 \(\vert\quad\vert\)를 써서 나타낸다.

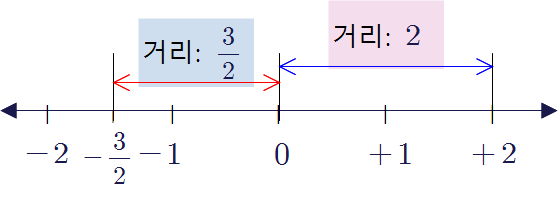
▶ \(+2\)를 나타내는 점은 원점으로부터의 거리가 \(2\)이므로 \(+2\)의 절댓값은 \(2\)이다. → \(\vert+2\vert=2\)

▶ \(-\dfrac32\)을 나타내는 점은 원점으로부터의 거리가 \(\dfrac32\)이므로 \(-\dfrac32\)의 절댓값은 \(\dfrac32\)이다. → \(\Big|-\dfrac32\Big|=\dfrac32\)

† \(0\)의 절댓값은 \(0\)이다.

† \(0\)을 제외한 모든 수는 절댓값이 같은 수가 한 쌍 존재한다.
 

❦ 유리수의 대소 관계

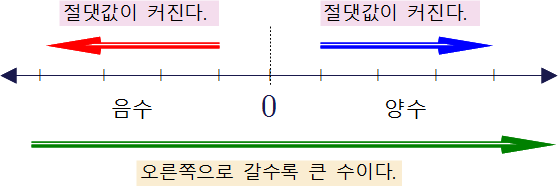
❧ 수를 수직선 위에 나타낼 때, 오른쪽에 있는 수가 왼쪽에 있는 수보다 크다. 따라서 수의 대소는 다음과 같이 정리할 수 있다.

▶ 양수끼리는 원점에서 멀리 떨어져 있는 수, 즉 절댓값이 큰 수가 크다.

▶ 음수끼리는 원점에서 멀리 떨어져 있는 수, 즉 절댓값이 큰 수가 작다.

❧ 부등호의 사용

• \(a>b\) : \(a\)는 \(b\)보다 크다.(초과)

• \(a<b\) : \(a\)는 \(b\)보다 작다.(미만)

• \(a\geq b\) : \(a\)는 \(b\)보다 크거나 같다.(이상)

• \(a\leq b\) : \(a\)는 \(b\)보다 작거나 같다.(이하)