❦ 최대공약수
❧ 공약수: 두 개 이상의 자연수의 공통인 약수
❧ 최대공약수: 공약수 중에서 가장 큰 수
(最大公約數, Greatest Common Divisor)
❧ 서로소: 최대공약수가 \(1\)이 두 자연수
▶ 서로소인 예: \(4\)와 \(7\), \(8\)과 \(13\) 등
❧ 최대공약수의 약수는 공약수이다.
▶ \(18\)의 약수: \(1,~2,~3,~6,~9,~18\)
\(24\)의 약수: \(1,~2,~3,~4,~6,~8,~12,~24\)
\(18,~24\)의 공약수: \(1,~2,~3,~6\)
\(18,~24\)의 최대공약수: \(6\)
→ \(18,~24\)의 공약수는 \(6\)의 약수이다.
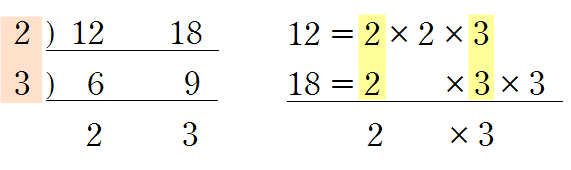
❦ 최소공배수
❧ 공배수: 두 개 이상의 자연수의 공통인 배수
❧ 최소공배수: 공배수 중에서 가장 작은 수
(最小公培數, Least Common Multiple)
❧ 두 개 이상의 자연수의 공배수는 그 수들의 최소공배수의 배수이다.
▶ \(4\)의 배수: \(4,~8,~12,~16,~20,~24,~28,~32,~36,~40,~44,~48,~\cdots\)
\(6\)의 배수: \(6,~12,~18,~24,~30,~36,~42,~48,~54,~\cdots\)
\(4\)와 \(6\)의 공배수: \(12,~24,~36,~48,~\cdots\)
\(4\)와 \(6\)의 최소공배수: \(12\)
→ \(4,~6\)의 공배수는 \(12\)의 배수이다.
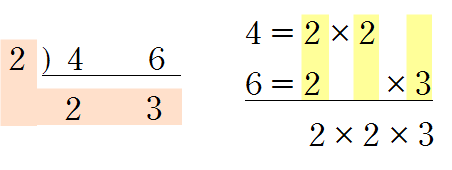
☞ 한 걸음 더
♠ 두 수의 최대공약수와 최소공배수를 구하는 계산기
♠ 최대공약수와 최소공배수의 관계
두 자연수 \(A\), \(B\)의 최대공약수가 \(G\)이고, 최소공배수가 \(L\)일 때,
\(\qquad A=a\times G,~B=b\times G(a,~b \)는 서로소)
라 하면 다음이 성립한다.
(1) \(L=a\times b\times G\)
(2) \(A\times B=L \times G\)
\[\begin{aligned}G\thinspace \underline{)\thinspace A\quad B \thinspace}\\a\quad\thinspace b\thinspace\thinspace\end{aligned}\]
♠ 수 이야기
-
완전수: 자기 자신을 제외한 약수들의 합이 자신이 되는 수
\(6=1+2+3\)
\(28=1+2+4+7+14\)
\(496=1+2+4+8+16+31+62+124+248\)
\(8128=1+2+4+8+16+32+64+127+254+508+1016+2032+4064\)
\(\cdots\) -
친화수: 자기 자신을 제외한 약수들의 합이 상대방 수가 되는 수
\(220=1+2+4+71+142\)
\(284=1+2+4+5+10+11+20+22+44+55+110\)
\((17296,~18416),~(1184,~1210),~\cdots\) -
혼약수: 자신과 \(1\)을 제외한 약수의 합이 상대방 수와 같은 두 수
\(48=3+5+15+25,~75=2+3+4+6+8+12+16+24\)
\((140,~195),~(1575,~1648),~(1050,~1925),~\cdots\)
♠ 배수 찾기
- \(2\)의 배수: 일의 자리의 숫자가 \(0\) 또는 \(2\)의 배수이다.
- \(3\)의 배수: 각 자리의 숫자의 합이 \(3\)의 배수이다.
- \(4\)의 배수: 끝의 두 자리가 \(00\) 또는 \(4\)의 배수이다.
- \(5\)의 배수: 일의 자리의 숫자가 \(0\) 또는 \(5\)이다.
- \(9\)의 배수: 각 자리의 숫자의 합이 \(9\)의 배수이다.
Copyright © 2003-2017 trsketch. All Rights Reserved. trsketch.dothome.co.kr
Saturday, July 18, 2015