❦ 소수와 합성수
❧ 소수: 자연수 \(2\)와 같이 \(1\)보다 큰 자연수 중에서 \(1\)과 그 수 자신만을 약수로 가지는 수
❧ 합성수: \(1\)보다 큰 자연수 중에서 \(1\)과 그 수 자신 이외에 또 다른 수를 약수로 가지는 수
▶ 소수의 예 : \(2,~3,~5,~7,~101\)
▶ 합성수의 예: \(6=2\times3,~12=4\times3\)
▶ \(1\)은 소수도 합성수도 아니다.

† 소수는 약수가 \(2\)개이다.
† 소수는 \(2\)를 제외하고 모두 홀수이다.
† 합성수는 약수가 \(3\)개 이상이다.
† 에라토스테네스의 체를 이용하면 비교적 작은 수에 대하여 소수를 쉽게 찾을 수 있다.
† 소수(素數, prime number)
소수(小數, decimal number)
<에라토스테네스의 체>
❦ 거듭제곱
❧ 거듭제곱: 같은 수나 문자를 여러 번 곱한 것을 간단히 나타낸 것
▶ 예) \(2\times2\times2=2^3,~a\times a\times a\times a=a^4\)
▶ [읽는 방법]
\(2^2 ~ \rightarrow ~2\)의 제곱, \(2^3 ~ \rightarrow ~2\)의 세제곱, \(2^4 ~ \rightarrow ~2\)의 네제곱
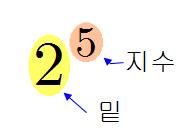
▶ 밑: 거듭제곱에서 여러 번 곱한 수나 문자
▶ 지수: 거듭제곱에서 여러 번 곱한 수나 문자의 곱한 횟수

† \(2^1=2\)
† \(2+2+2+2+2=2\times5\)
\(2\times2\times2\times2\times2=2^5\)
❦ 소인수분해
❧ 인수: 자연수 \(a,~b,~c\)에 대하여 \(a=b\times c\)일 때, \(b,~c\)를 \(a\)의 인수라고 한다.
❧ 소인수: 소수인 인수
▶ 예) \(6=1\times6,~6=2\times 3\)이므로 \(6\)의 소인수는 \(2,~3\)이다.
❧ 소인수분해: 자연수를 소인수의 곱으로 나타내는 것
▶ 예) \(12=2\times6=2\times2\times3=\bbox[yellow]{ 2^2\times3 }\)
❧ 소인수분해를 이용한 약수의 개수
▶ 예) \(20=2\times10=2\times2\times5=2^2\times5\)
\(\begin {aligned} 2\underline {)~20~} \\2\underline {)~10~} \\ 5\thinspace\thinspace\end {aligned} \qquad\begin {aligned} 20=2^2\times5 \end {aligned}\)
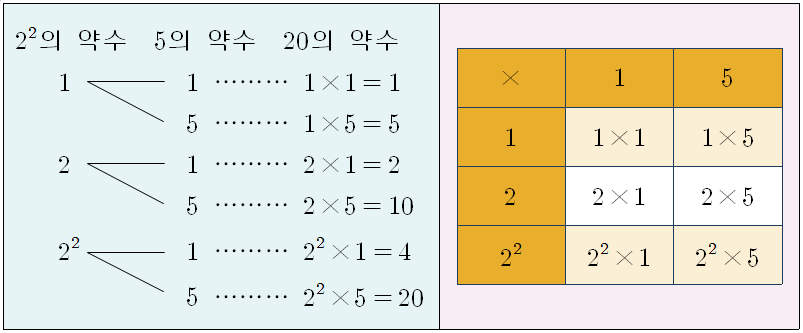

† 소인수분해한 결과는 소인수의 순서를 생각하지 않는다면 오직 한 가지 뿐이다.
☞ 한 걸음 더
♠ 작은 수에 대하여 소수 찾는 계산기
♠소수에 관한 여러 가지 문제들
- 소수는 무한할까?(기원전 300년 경에 해결됨)
- 아주 큰 수에 대하여 이 수가 소수인지 아닌지를 판별하는 방법은 있는가?
- 쌍둥이 소수(\(3\)과 \(5\), \(11\)과 \(13\)처럼 \(p\)와 \(p+2\) 형태의 소수)가 무한한가?
- 골드바흐의 추측: \(2\)를 제외한 모든 짝수는 두 소수의 합으로 나타낼 수 있는가?
- \(n^2 +1\)형태의 소수는 무수히 많은가?
- \(2^{ 2^n }+1\)꼴의 소수는 무수히 많은가?(페르마의 소수)
- 기타 등등
Free JavaScripts provided by The JavaScript Source
Copyright © 2003-2017 trsketch. All Rights Reserved. trsketch.dothome.co.kr
Saturday, July 18, 2015